题目内容
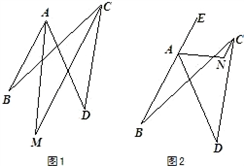
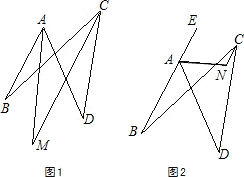 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.(1)∠BAD和∠BCD的角平分线交于点M(如图1),求∠AMC的大小;
(2)点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图2),则∠ANC=
分析:(1)根据题意,设AD与BC交于点F,BC与AM交于P,∠CFD=x°,根据三角形的内角和定理以及角平分线的定义可以利用x表示出∠BCM的值,以及∠APB的度数,即∠CPM的度数,在△CPM中,利用三角形的内角和定理,即可求∠AMC.
(2)设AD、BC交于点F,设∠AFB=x°,设AN与BC交于点R,利用三角形的内角和定理以及三角形外角的性质,利用x表示出∠RCN以及∠CRN的度数,然后在△CNR中,利用三角形内角和定理即可求解.
(2)设AD、BC交于点F,设∠AFB=x°,设AN与BC交于点R,利用三角形的内角和定理以及三角形外角的性质,利用x表示出∠RCN以及∠CRN的度数,然后在△CNR中,利用三角形内角和定理即可求解.
解答:解:(1)如图1,设AD与BC交于点F,BC与AM交于P,AD与CM交于Q,设∠CFD=x°,则∠AFB=∠CFD=x度,
△CFD中∠BCD=180°-∠ADC-∠CFD=180°-42°-x=138°-x,
∵CM平分∠BCD得到:
∠BCM=
∠BCD=69°-
x,
同理:∠BAM=∠MAD=78°-
x,
在△ABP中利用三角形内角和定理得到:
∠APB=180°-24°-(78°-
x)=78°+
x,
则∠CPM=∠APB=180°-24°-(78°-
x)=78°+
x,
在△CPM中三内角的和是180°,
即:(69°-
x)+(78°+
x)+∠AMC=180°,
则∠AMC=33°;
(2)设AD、BC交于点F,设∠AFB=x°,设AN与BC交于点R,(见图2)
∠EAD=∠B+∠AFB=24°+x,则∠RAD=∠EAN=12°+
x,
∵∠AFB=∠ARF+∠RAD,
∴∠ARB=∠CRN=∠EAN-∠B=
x-12°,
又∵由(1)可知∠BCN=69°-
x,
在△CNR中利用三角形内角和定理:
(
x-12°)+(69°-
x)+∠ANC=180°,
解得∠ANC=123°.
△CFD中∠BCD=180°-∠ADC-∠CFD=180°-42°-x=138°-x,
∵CM平分∠BCD得到:
∠BCM=
| 1 |
| 2 |
| 1 |
| 2 |
同理:∠BAM=∠MAD=78°-
| 1 |
| 2 |
在△ABP中利用三角形内角和定理得到:

∠APB=180°-24°-(78°-
| 1 |
| 2 |
| 1 |
| 2 |
则∠CPM=∠APB=180°-24°-(78°-
| 1 |
| 2 |
| 1 |
| 2 |
在△CPM中三内角的和是180°,
即:(69°-
| 1 |
| 2 |
| 1 |
| 2 |
则∠AMC=33°;
(2)设AD、BC交于点F,设∠AFB=x°,设AN与BC交于点R,(见图2)
∠EAD=∠B+∠AFB=24°+x,则∠RAD=∠EAN=12°+
| 1 |
| 2 |
∵∠AFB=∠ARF+∠RAD,
∴∠ARB=∠CRN=∠EAN-∠B=
| 1 |
| 2 |
又∵由(1)可知∠BCN=69°-
| 1 |
| 2 |
在△CNR中利用三角形内角和定理:
(
| 1 |
| 2 |
| 1 |
| 2 |
解得∠ANC=123°.
点评:在解题过程中如果需要一个量的值时,可以先把它设出,在解题过程中用所设的未知数表示,设的量可能也不需求出.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=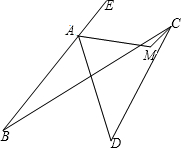 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=