题目内容
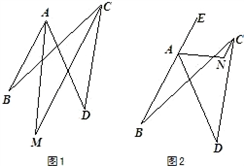
 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=| 180°+m°+n° |
| 2 |
| 180°+m°+n° |
| 2 |
分析:先设∠AFB=x,在由三角形外角的性质及三角形内角和定理用x表示出∠DAR、∠CRN及∠RCN的度数,再根据三角形内角和定理即可得出结论.
解答: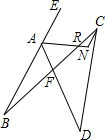 解:设∠AFB=x,
解:设∠AFB=x,
∵AN是∠EAD的平分线,
∴∠DAR=
=
,
∴∠CRN=∠ANF=180°-∠DAR-∠AFR=180°-
-(180°-x)=
,
∵∠DFC=∠AFB=x,∠ADC=n°,CN是∠BCD的平分线,
∴∠RCN=
=
,
在△CNR中,
∠ANC+∠RCN+∠CRN=180°,即∠ANC=180°-
-
=
.
故答案为:
.
 解:设∠AFB=x,
解:设∠AFB=x,∵AN是∠EAD的平分线,
∴∠DAR=
| ∠ABC+∠AFB |
| 2 |
| m°+x |
| 2 |
∴∠CRN=∠ANF=180°-∠DAR-∠AFR=180°-
| m°+x |
| 2 |
| x-m° |
| 2 |
∵∠DFC=∠AFB=x,∠ADC=n°,CN是∠BCD的平分线,
∴∠RCN=
| 180°-∠ADN-∠DFC |
| 2 |
| 180°-n°-x |
| 2 |
在△CNR中,
∠ANC+∠RCN+∠CRN=180°,即∠ANC=180°-
| 180°-n°-x |
| 2 |
| x-m° |
| 2 |
| 180°+m°+n° |
| 2 |
故答案为:
| 180°+m°+n° |
| 2 |
点评:本题考查的是三角形外角的性质,三角形内角和定理及角平分线的性质,根据题意设∠AFB的度数为x,再用x表示出∠DAR、∠CRN及∠RCN的度数是解答此题的关键.

练习册系列答案
相关题目
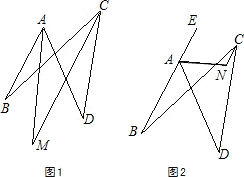 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.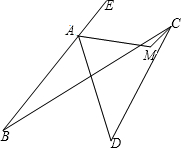 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=