题目内容
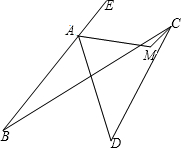 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=123
123
°.分析:先设AD、BC交于点F,∠ABF=x.根据三角形的外角的性质,可得∠EAD=∠B+∠AFB,再根据角平分线的定义知∠EAM=12+
x,即可求得∠CRM的值,由三角形的内角和定理,易求∠AMC.
| 1 |
| 2 |
解答: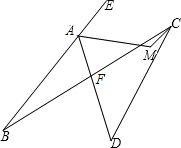 解:设AD、BC交于点F,AM与BC交于点R,∠AFB=x.
解:设AD、BC交于点F,AM与BC交于点R,∠AFB=x.
∠EAD=∠B+∠AFB=24+x,则∠EAM=12+
x,
则∠ARB=∠CRM=
x-12,
又∵∠BCM=69-
x,
设在△CMR中利用三角形内角和定理:
(
x-12)+(69-
x)+∠AMC=180,
解得∠AMC=123°.
故应填:123.
 解:设AD、BC交于点F,AM与BC交于点R,∠AFB=x.
解:设AD、BC交于点F,AM与BC交于点R,∠AFB=x.∠EAD=∠B+∠AFB=24+x,则∠EAM=12+
| 1 |
| 2 |
则∠ARB=∠CRM=
| 1 |
| 2 |
又∵∠BCM=69-
| 1 |
| 2 |
设在△CMR中利用三角形内角和定理:
(
| 1 |
| 2 |
| 1 |
| 2 |
解得∠AMC=123°.
故应填:123.
点评:本题主要考查了三角形的外角性质和三角形的内角和定理.在解题过程中如果需要一个量的值时,可以先把它设出,在解题过程中用所设的未知数表示,设的量可能也不需求出.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
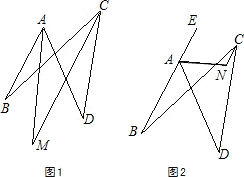 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°.
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=24°,∠ADC=42°. 平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=
平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠ABC=m°,∠ADC=n°.点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线交于点N(如图),则∠ANC=
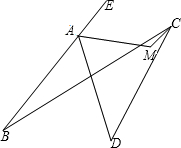 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=________°.
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=________°.