题目内容
12. 某商店销售甲、乙两种商品,现有如下信息:
某商店销售甲、乙两种商品,现有如下信息:请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价-进货单价)
分析 (1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;
(2)根据降价后甲每天卖出:(500+$\frac{m}{0.1}$×100)件,每件降价后每件利润为:(1-m)元;即可得出总利润,利用一元二次方程解法求出即可.
解答 解:(1)设甲商品进货单价x元,乙商品进货单价y元.
依题意,得
$\left\{\begin{array}{l}{x+y=3}\\{3x+2y=7}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
答:甲商品进货单价为1元,乙商品进货单价为2元.
(2)依题意,得
(2-m-1)•(500+1000m)+(3-2)×1300=1800
(1-m)•(500+1000m)=500
即2m2-m=0
∴m1=0.5,m2=0
∵m>0
∴m=0不合舍去,即m=0.5
答:当m=0.5时,商店获取的总利润为1800元.
点评 此题主要考查了一元二次方程的应用,注意利用总利润=商品的单件利润×所卖商品件数是解决问题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
3.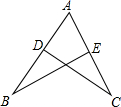 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )| A. | ∠B=∠C | B. | BE=CD | C. | BD=CE | D. | ∠ADC=∠AEB |
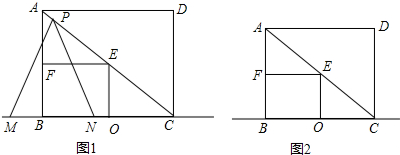
 如图,C、D是线段AB上的两点,点D是AC中点,AB=10,AD=4,则DB=6.
如图,C、D是线段AB上的两点,点D是AC中点,AB=10,AD=4,则DB=6.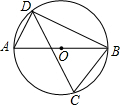 如图,点A、B、C、D在⊙O上,AB为⊙O的直径,∠C=60°,AD=3,求△ABD的面积.
如图,点A、B、C、D在⊙O上,AB为⊙O的直径,∠C=60°,AD=3,求△ABD的面积. 如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么?
如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么?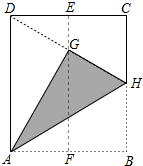 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.
如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.