��Ŀ����
8����֪�ı���ABCD�У�EF�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G����1����ͼ1�����ı���ABCD�������Σ���DE��CF����֤��DE=CF��
��2����ͼ2�����ı���ABCD�Ǿ��Σ���DE��CF����֤��$\frac{DE}{CF}$=$\frac{AD}{CD}$��
��3����ͼ3�����ı���ABCD��ƽ���ı��Σ�����B=��EGFʱ���ڣ�2���ʵĽ����Ƿ����������������֤����������������˵�����ɣ�
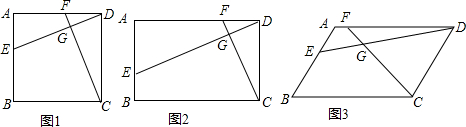
���� ��1�����ı���ABCDΪ�����Σ����������ε����ʵõ�һ�Խ�Ϊֱ�ǣ���ȣ���AD=DC������ͬ�ǵ������ȵõ�һ�Խ���ȣ�����AAS�õ�������ADE��������DCFȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
��2�����ı���ABCDΪ���Σ��õ�һ��ֱ����ȣ�����ͬ�ǵ������ȵõ�һ�Խ���ȣ��������Խ���ȵ����������Ƶõ�������ADE��������DCF���ƣ��������������ζ�Ӧ�߳ɱ������ɵ�֤��
��3������B=��EGFʱ��$\frac{DE}{CF}$=$\frac{AD}{DC}$����������Ϊ����ͼ3����AD���ӳ�����ȡ��M��ʹCM=CF������ƽ���ߵ����ʣ��Լ�ͬ�ǵIJ�����ȵõ�������ADE��������DCM���ƣ��������������ζ�Ӧ�߳ɱ������ɵ�֤��
��� ��1��֤�������ı���ABCD�������Σ�
���A=��ADC=90�㣬AD=DC��
���ADE+��AED=90�㣬
��DE��CF��
���ADE+��CFD=90�㣬
���AED=��CFD��
���ADE�ա�DCF��
��DE=CF��
��2��֤�������ı���ABCD�Ǿ��Σ�
���A=��ADC=90�㣬
��DE��CF��
���ADE+��CFD=90�㣬��DCF+��CFD=90�㣬
���ADE=��DCF��
���ADE�ס�DCF��
��$\frac{DE}{CF}$=$\frac{AD}{DC}$��
��3���⣺����B=��EGFʱ��$\frac{DE}{CF}$=$\frac{AD}{DC}$������
֤������ͼ3����AD���ӳ�����ȡ��M��ʹCM=CF��
���CMF=��CFM��
��AB��CD��
���A=��CDM��
��AD��BC��
���B+��A=180�㣬
�ߡ�B=��EGF��
���EGF+��A=180�㣬
���AED=��CFM=��CMF��
���ADE�ס�DCM��
��$\frac{DE}{CM}$=$\frac{AD}{DC}$����$\frac{DE}{CF}$=$\frac{AD}{DC}$��
���� ���������������ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ����������ε��ж������ʣ�ƽ���ı��ε����ʣ��Լ�ƽ���ߵ����ʣ������������������ε��ж��������ǽⱾ��Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��-x-y����x+y�� | B�� | ��2x-y����y-2x�� | C�� | ��1-$\frac{1}{2}$x����-1-$\frac{1}{2}$x�� | D�� | ��3x+y����x-3y�� |
| A�� | a3+a3=a6 | B�� | ��ab��2=a2b2 | C�� | 2��a+1��=2a+1 | D�� | a6��a3=a2 |




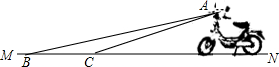 ���··ͨ�綯�����¿�����һ�ֵ綯����ͼ�����Ĵ��A����Ĺ���AB��AC �����MN ���е���Ƿֱ�Ϊ8���10�㣬���A�����ľ���Ϊ1m��ó������������Ŀ���BC��1.4m�����������������أ�
���··ͨ�綯�����¿�����һ�ֵ綯����ͼ�����Ĵ��A����Ĺ���AB��AC �����MN ���е���Ƿֱ�Ϊ8���10�㣬���A�����ľ���Ϊ1m��ó������������Ŀ���BC��1.4m�����������������أ�