题目内容
一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 .
考点:多边形内角与外角
专题:
分析:先求出新多边形的边数,再根据截去一个角后的多边形与原多边形的边数相等,多1,少1三种情况进行讨论.
解答:解:设新多边形的边数是n,则(n-2)•180°=2520°,
解得n=16,
∵截去一个角后的多边形与原多边形的边数可以相等,多1或少1,
∴原多边形的边数是15,16,17.
故答案为:15,16,17.
解得n=16,
∵截去一个角后的多边形与原多边形的边数可以相等,多1或少1,
∴原多边形的边数是15,16,17.
故答案为:15,16,17.
点评:本题考查了多边形的内角和定理,难点在于截去一个角后的多边形与原多边形的边数相等,多1,少1,有这么三种情况.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列事件中,必然事件是( )
| A、掷一枚硬币,着地时反面向上 |
| B、星期天一定是晴天 |
| C、打开电视机,正在播放动画片 |
| D、在标准大气压下,水加热到100℃会沸腾 |
点P(2,3)关于原点的对称点Q的坐标是( )
| A、(-2,3) |
| B、(2,-3) |
| C、(3,2) |
| D、(-2,-3) |
某校8名女生的体重(单位:kg)为:35,41,42,40,41,42,42,45,则这组数据的众数和中位数(单位:kg)分别为( )
| A、41与41 |
| B、42与41 |
| C、41与41.5 |
| D、42与41.5 |
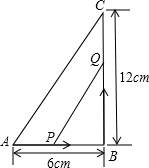 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,Q从点B开始沿BC边向C点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,Q从点B开始沿BC边向C点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?