题目内容
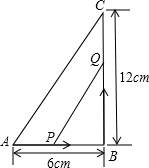如图，在△ABC中，∠B=90°，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，Q从点B开始沿BC边向C点以2cm/s的速度移动，如果点P、Q分别从A、B同时出发，几秒钟后，△PBQ的面积等于8cm2？考点：一元二次方程的应用
专题：几何动点问题
分析：根据直角三角形的面积公式和路程=速度×时间进行求解即可．
解答：解：设x秒钟后，△PBQ的面积等于8cm2，由题意可得：
2x（6-x）÷2=8，
解得x1=2，x2=4．
答：2或4秒钟后，△PBQ的面积等于8cm2．
2x（6-x）÷2=8，
解得x1=2，x2=4．
答：2或4秒钟后，△PBQ的面积等于8cm2．
点评：本题考查了一元二次方程的应用，抓住关键描述语“△PBQ的面积等于8cm2”，找到等量关系是解决问题的关键．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
方程（x-2）2=（3-2x）2可化为（ ）
| A、x-2=3-2x |
| B、x-2=2x-3 |
| C、x-2=3-2x或x-2=2x-3 |
| D、以上都不对 |
在圆的面积公式S=πr2中，s与r的关系是（ ）
| A、一次函数关系 |
| B、正比例函数关系 |
| C、二次函数关系 |
| D、不是函数关系 |
如图，已知动点A在函数y=
把两根钢条AA、BB的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳），如图，若得AB=7厘米，则槽宽为抛物线y=-（x-1）2+4上部分点的横坐标y=-（x-1）2+2，纵坐标y=-（x+1）2+4的对应值如下表：
从上表可知，下列说法中正确的是（ ）
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A、抛物线与x轴的一个交点为（4，0） | ||
| B、函数y=ax2+bx+c的最大值为6 | ||
C、抛物线的对称轴是x=
| ||
| D、在对称轴右侧，y随x增大而增大 |