题目内容
2. 小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证.
小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证.(1)在方框中填空,以补全已知和求证;
已知:如图,在四边形ABCD中,BC=AD,AB=CD.
求证:四边形ABCD是平行四边形.
(2)写出证明过程:
分析 (1)题设作为已知条件,结论作为求证即可解决问题;
(2)连接BD,只要证明△ABD≌△CDB.推出∠1=∠2,∠3=∠4.推出AB∥CD,AD∥CB即可;
解答 解:(1)AB=CD 平行四边形.
故答案为AB=CD,平行四边形.
(2)证明:连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABC D是平行四边形.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握命题的证明方法,学会写已知求证,属于中考常考题型.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
12. 如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )
如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )
 如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )
如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{7}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{7}$ |
17.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线相等且互相垂直的四边形是菱形 | |
| D. | 对角线相等且互相垂直的平行四边形是正方形 |
12.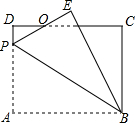 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )| A. | 4.8 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 3$\sqrt{3}$ |
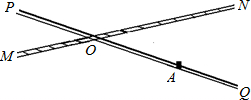 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为多少?
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为多少?
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.