题目内容
14.计算:(1)(-$\frac{2}{3}$m+$\frac{1}{4}$n2)(-$\frac{1}{4}$n2-$\frac{2}{3}$m)
(2)(-6a2b5c)÷(-2ab2)2.
分析 (1)原式利用平方差公式计算即可得到结果;
(2)原式先利用幂的乘方与积的乘方运算法则计算,再利用单项式除以单项式法则计算即可得到结果.
解答 解:(1)原式=(-$\frac{2}{3}$m)2-($\frac{1}{4}$n2)2=$\frac{4}{9}$m2-$\frac{1}{16}$n4;
(2)原式=(-6a2b5c)÷(4a2b4)=-$\frac{3}{2}$bc.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
9.($\frac{2}{3}$)2014•(-1.5)2015=( )
| A. | ($\frac{2}{3}$)2014 | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | (-$\frac{3}{2}$)2014 |
6.已知$\frac{2a}{3b+3c}$=$\frac{2b}{3c+3a}$=$\frac{2c}{3a+3b}$=k,则k的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$或-$\frac{2}{3}$ | D. | $\frac{2}{3}$或-1 |
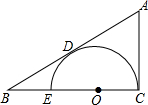 已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长.
已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC:CB=1:3,AD=4.求BE的长. 如图,在长方形中.用式子表示阴影部分的面积.并求出当a=2,b=2时,阴影部分的面积.
如图,在长方形中.用式子表示阴影部分的面积.并求出当a=2,b=2时,阴影部分的面积.