题目内容
选择适当方法解下列方程:
(1)x2-5x+1=0(用配方法);
(2)3(x-2)2=x(x-2);
(3)2x2-2
x-5=0(公式法);
(4)(y+2)2=(3y-1)2.
(1)x2-5x+1=0(用配方法);
(2)3(x-2)2=x(x-2);
(3)2x2-2
| 2 |
(4)(y+2)2=(3y-1)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:(1)利用配方法得到(x-
)2=
,然后根据直接开平方法求解;
(2)先变形得到3(x-2)2-x(x-2)=0,然后利用因式分解法解方程;
(3)先计算判别式的值,然后利用求根公式法求解;
(4)先变形得到(y+2)2-(3y-1)2=0,然后利用因式分解法解方程.
| 5 |
| 2 |
| 21 |
| 4 |
(2)先变形得到3(x-2)2-x(x-2)=0,然后利用因式分解法解方程;
(3)先计算判别式的值,然后利用求根公式法求解;
(4)先变形得到(y+2)2-(3y-1)2=0,然后利用因式分解法解方程.
解答:解:(1)x2-5x=-1,
x2-5x+(
)2=-1+(
)2,
(x-
)2=
,
x-
=±
,
所以x1=
,x2=
;
(2)3(x-2)2-x(x-2)=0,
(x-2)(3x-6-x)=0,
所以x1=2,x2=3;
(3)△=(-2
)2-4×2×(-5)=48
x=
=
=
,
所以x1=
,x2=
;
(4)(y+2)2-(3y-1)2=0,
(y+2+3y-1)(y+2-3y+1)=0,
y+2+3y-1=0或y+2-3y+1=0,
所以y1=-
,y2=
.
x2-5x+(
| 5 |
| 2 |
| 5 |
| 2 |
(x-
| 5 |
| 2 |
| 21 |
| 4 |
x-
| 5 |
| 2 |
| ||
| 2 |
所以x1=
5+
| ||
| 2 |
5-
| ||
| 2 |
(2)3(x-2)2-x(x-2)=0,
(x-2)(3x-6-x)=0,
所以x1=2,x2=3;
(3)△=(-2
| 2 |
x=
2
| ||||
| 2×2 |
2
| ||||
| 4 |
| ||||
| 2 |
所以x1=
| ||||
| 2 |
| ||||
| 2 |
(4)(y+2)2-(3y-1)2=0,
(y+2+3y-1)(y+2-3y+1)=0,
y+2+3y-1=0或y+2-3y+1=0,
所以y1=-
| 1 |
| 4 |
| 3 |
| 2 |
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了公式法和配方法解一元二次方程.

练习册系列答案
相关题目
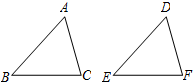 如图,给出下列四组条件,其中,不能使△ABC≌△DEF的条件是( )
如图,给出下列四组条件,其中,不能使△ABC≌△DEF的条件是( )| A、AB=DE,BC=EF,AC=DF |
| B、AB=DE,∠B=∠E,BC=EF |
| C、∠B=∠E,BC=EF,∠C=∠F |
| D、AB=DE,AC=DF,∠B=∠E |
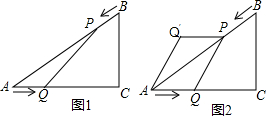 如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题: