题目内容
如图①,A(4,0),C(0,n)分别是x和y轴上的点,n>0,以OA,OC为边在第一象限内作矩形OABC,对角线OB,AC,交于点D双曲线y=
(x>0,k>0)交边BC于G,交边AB于H.
(1)设直线AC的函数关系式为y=qx+p,请用含n的代数式表示q和p.
(2)求证:
=
;
(3)如图②,若上述双曲线经过点D,判断点D是否是双曲线与直线AC唯一的交点,请说明理由.

| k |
| x |
(1)设直线AC的函数关系式为y=qx+p,请用含n的代数式表示q和p.
(2)求证:
| BG |
| BC |
| BH |
| BA |
(3)如图②,若上述双曲线经过点D,判断点D是否是双曲线与直线AC唯一的交点,请说明理由.

考点:反比例函数综合题
专题:
分析:(1)设y=qx+p,将点A(4,0)和点C(0,n)代入即可用含n的代数式表示q和p;
(2)根据点G和点H均在y=
上,设H(4,
),G(
,n)从而得到BG=4-
=
,BH=n-
=
,利用
=
=
,即可证得
=
;
(3)设D点的坐标为:(2,
),然后得到y=
,联立组成方程组即可得整理得到方程-x2+4x=4,根据方程有两个相等的实数根判断点D是双曲线与直线AC唯一的交点.
(2)根据点G和点H均在y=
| k |
| x |
| k |
| 4 |
| k |
| n |
| k |
| n |
| 4n-k |
| n |
| k |
| 4 |
| 4n-k |
| 4 |
| BG |
| BH |
| 4 |
| n |
| BC |
| AB |
| BG |
| BC |
| BH |
| BA |
(3)设D点的坐标为:(2,
| n |
| 2 |
| n |
| x |
解答:解:(1)设y=qx+p
由A(4,0)得0=4q+p,
由C(0,n)得n=p,
∴q=-
,p=n;
(2)∵点G和点H均在y=
上,
∴设H(4,
),G(
,n)
所以BG=4-
=
,BH=n-
=
,
∴
=
=
,
即
=
;
(3)设D点的坐标为:(2,
),
当x=2,y=
时,
=
,k=n,
∴y=
,
由
得-
x+n=
即-nx2+4nx=4n,
-x2+4x=4,
解得:x1=x2=2,
∴点D是双曲线与直线AC唯一的交点.
由A(4,0)得0=4q+p,
由C(0,n)得n=p,
∴q=-
| n |
| 4 |
(2)∵点G和点H均在y=
| k |
| x |
∴设H(4,
| k |
| 4 |
| k |
| n |
所以BG=4-
| k |
| n |
| 4n-k |
| n |
| k |
| 4 |
| 4n-k |
| 4 |
∴
| BG |
| BH |
| 4 |
| n |
| BC |
| AB |
即
| BG |
| BC |
| BH |
| BA |
(3)设D点的坐标为:(2,
| n |
| 2 |
当x=2,y=
| n |
| 2 |
| n |
| 2 |
| k |
| 2 |
∴y=
| n |
| x |
由
|
得-
| n |
| 4 |
| n |
| x |
即-nx2+4nx=4n,
-x2+4x=4,
解得:x1=x2=2,
∴点D是双曲线与直线AC唯一的交点.
点评:本题考查了反比例函数的综合知识,解题的关键是用未知数将点的坐标表示出来,难度中等偏上.

练习册系列答案
相关题目
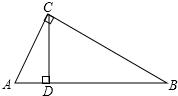 如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )| A、3cm | B、6cm |
| C、9cm | D、12cm |
下列图形经过折叠不能围成一个几何体的是( )
A、 |
B、 |
C、 |
D、 |
下面两点中,关于x轴对称的是( )
| A、(1,-3)和(-1,-3) |
| B、(3,-5)和(-3,5) |
| C、(5,-4)和(5,4) |
| D、(-2,4)和(2,4) |
