题目内容
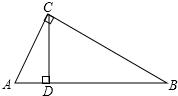如图，在Rt△ABC中，∠C=90°，∠B=30°，CD是斜边AB上的高，AD=3cm，则AB的长度是（ ）| A、3cm | B、6cm |
| C、9cm | D、12cm |
考点：含30度角的直角三角形
专题：
分析：先求出∠ACD=30°，然后根据30°所对的直角边等于斜边的一半解答．
解答：
解：在Rt△ABC中，
∵CD是斜边AB上的高，
∴∠ADC=90°，
∴∠ACD=∠B=30°（同角的余角相等），
∵AD=3cm，
在Rt△ACD中，AC=2AD=6cm，
在Rt△ABC中，AB=2AC=12cm．
∴AB的长度是12cm．
故选D．
解：在Rt△ABC中，∵CD是斜边AB上的高，
∴∠ADC=90°，
∴∠ACD=∠B=30°（同角的余角相等），
∵AD=3cm，
在Rt△ACD中，AC=2AD=6cm，
在Rt△ABC中，AB=2AC=12cm．
∴AB的长度是12cm．
故选D．
点评：本题主要考查直角三角形30°角所对的直角边等于斜边的一半的性质．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB+BC=BE，则∠B的度数是（ ）| A、45° | B、50° |
| C、55° | D、60° |
下列各式中，能用平方差公式分解因式的是（ ）
| A、a2+9 |
| B、a2-y |
| C、-a2+9 |
| D、-a2-9 |
如果反比例函数y=
的图象经过点（-2，-3），则k的值是（ ）
| k-1 |
| x |
| A、7 | B、5 | C、-6 | D、6 |
已知⊙O的半径是5，直线l是⊙O的切线，P是l上的任一点，那么（ ）
| A、0＜OP＜5 | B、OP=5 |
| C、OP＞5 | D、OP≥5 |
下列长度的各种线段，可以组成三角形的是（ ）
| A、1，2，3 |
| B、1，5，5 |
| C、3，3，6 |
| D、4，5，10 |
如图，用直角曲尺检查半圆形的工件是否合格，运用到的道理是（ ）
| A、同弧所对的圆周角相等 |
| B、直径是圆中最大的弦 |
| C、90°圆周角所对的弦是直径 |
| D、圆上各点到圆心的距离相等 |
若关于x的方程ax=6+x的解是整数，则满足这个方程的a的值有几个（ ）
| A、5个 | B、6个 | C、7个 | D、8个 |
