题目内容
15.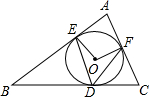 如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 65° |
分析 根据三角形的内角和定理求出∠A,根据多边形的内角和定理求出∠EOF,根据圆周角定理求出∠EDF即可.
解答 解:∵∠A+∠B+∠C=180°,∠B=45°,∠C=65°,
∴∠A=70°,
∵⊙O内切于△ABC,切点分别为D、E、F,
∴∠OEA=∠OFA=90°,
∴∠EOF=360°-∠A-∠OEA-∠OFA=110°,
∴∠EDF=$\frac{1}{2}$∠EOF=55°.
故选:C.
点评 本题主要考查对三角形的内切圆与内心,三角形的内角和定理,多边形的内角和定理,圆周角定理等知识点的理解和掌握,能求出∠EOF的度数是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列计算正确的是( )
| A. | 3a-2a=1 | B. | 2x2y-xy2=xy2 | C. | 3a2+5a2=8a4 | D. | 3ax-2xa=ax |
20.下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )
| A. | 2,4,2$\sqrt{3}$ | B. | 1,1,$\sqrt{2}$ | C. | 1,2,$\sqrt{5}$ | D. | $\sqrt{3}$,2,$\sqrt{5}$ |
7.下面是2013年一月份的日历,小明在日历上圈出一个竖列且相邻的三个日期,算出它们的和是48,则这三天分别是( )
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
| A. | 6,16,26 | B. | 9,16,23 | C. | 15,16,17 | D. | 不确定 |
5.下列说法中,错误的是( )
| A. | 单项式-a2bc的系数是-1,次数是4 | |
| B. | 整式可分为单独一个数字、单独一个字母、单项式、多项式 | |
| C. | 多项式4a2-3b是二次二项式 | |
| D. | 4(3-x)2与-2(x-3)2可以看作是同类项 |
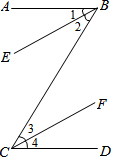 补全下题的证明过程(括号里面填依据).
补全下题的证明过程(括号里面填依据).