题目内容
 5、如图,△ABD中,∠BAD=45°,AE⊥BD于E,DF⊥AB于F,交AE于G,BE=4,DE=3,则AG=
5、如图,△ABD中,∠BAD=45°,AE⊥BD于E,DF⊥AB于F,交AE于G,BE=4,DE=3,则AG=7
.分析:由∠BAD=45,DF⊥AB于F得AF=DF,利用等角∠AGF=DGE的余角相等可得∠BAE=∠BDF,则可证得△AGF≌△DBF(AAS),则AG=BD=BE+DE=7.
解答:解:由∠BAD=45°,DF⊥AB于F则△ADF是等腰直角三角形,
所以AF=DF,
又∵∠AGF=∠DGE,AE⊥BD于E,
∴∠FAG=∠GDE,
利用等角(或同角)的余角相等可证得∠BAE=∠BDF,
又∠AFG=∠DFB=90°,
可证得△AGF≌△DBF(AAS),
所以AG=BD=BE+DE=7.
所以AF=DF,
又∵∠AGF=∠DGE,AE⊥BD于E,
∴∠FAG=∠GDE,
利用等角(或同角)的余角相等可证得∠BAE=∠BDF,
又∠AFG=∠DFB=90°,
可证得△AGF≌△DBF(AAS),
所以AG=BD=BE+DE=7.
点评:这是一道全等三角形的判定和直角三角形性质的综合,易出题,应该掌握.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
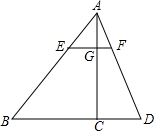 (2012•呼伦贝尔)如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=
(2012•呼伦贝尔)如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG= 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求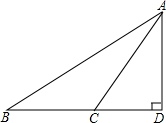 如图,△ABD中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,AD的长为( )
如图,△ABD中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,AD的长为( ) 写出推理步骤:如图,△ABD中,AB=BC=AD,则∠α和∠β有什么数量关系?请结合已知条件推理出一个等式.
写出推理步骤:如图,△ABD中,AB=BC=AD,则∠α和∠β有什么数量关系?请结合已知条件推理出一个等式.