题目内容
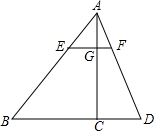（2012•呼伦贝尔）如图，△ABD中，EF∥BD交AB于点E、交AD于点F，AC交EF于点G、交BD于点C，S△AEG=| 1 |
| 8 |
| AF |
| AD |
分析：利用相似三角形△AEG∽△ABC的性质证得
=(
)2=
；然后根据平行线截线段成比例求得
=
=
．
| S△AEG |
| SABC |
| AE |
| AB |
| 1 |
| 9 |
| AF |
| AD |
| AE |
| AB |
| 1 |
| 3 |
解答：解：∵S△AEG=
S四边形EBCG，
∴S△AEG=
S△ABC，
又∵EF∥BD，
∴
=
（平行线截线段成比例），∠EAG=∠BAC，
∴△AEG∽△ABC，
∴
=(
)2=
（相似三角形面积的比等于相似比的平方）；
∴
=
；
∴
=
=
．
故选D．
| 1 |
| 8 |
∴S△AEG=
| 1 |
| 9 |
又∵EF∥BD，
∴
| AE |
| AB |
| AG |
| AC |
∴△AEG∽△ABC，
∴
| S△AEG |
| SABC |
| AE |
| AB |
| 1 |
| 9 |
∴
| AE |
| AB |
| 1 |
| 3 |
∴
| AF |
| AD |
| AE |
| AB |
| 1 |
| 3 |
故选D．
点评：本题考查了相似三角形的判定与性质、平行线分线段成比例．平行于三角形一边的直线截其它两边所在的直线，截得的三角形与原三角形相似．
练习册系列答案
相关题目
