题目内容
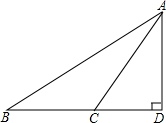如图，△ABD中，∠D=90°，C是BD上一点，已知CB=9，AB=17，AC=10，AD的长为（ ）分析：在Rt△ABD和Rt△ACD中，利用勾股定理列式表示出CD，然后解方程即可．
解答：解：在Rt△ABD中，9+CD=
，
和Rt△ACD中，CD=
，
∴9+
=
，
两边平方得，81+18
+100-AD2=289-AD2，
∴
=6，
两边平方得，100-AD2=36，
解得AD=8．
故选D．
| 172-AD2 |
和Rt△ACD中，CD=
| 102-AD2 |
∴9+
| 102-AD2 |
| 172-AD2 |
两边平方得，81+18
| 102-AD2 |
∴
| 102-AD2 |
两边平方得，100-AD2=36，
解得AD=8．
故选D．
点评：本题考查了勾股定理，在两个直角三角形中列式表示出CD是解题的关键，要注意无理方程的求解技巧．
练习册系列答案
相关题目
5、如图，△ABD中，∠BAD=45°，AE⊥BD于E，DF⊥AB于F，交AE于G，BE=4，DE=3，则AG=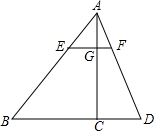
（2012•呼伦贝尔）如图，△ABD中，EF∥BD交AB于点E、交AD于点F，AC交EF于点G、交BD于点C，S△AEG=
如图，△ABD中，点C、F分别为BD、AB上一点，AC、DF交于E，且CD=2BC，AE=2CE．求
写出推理步骤：如图，△ABD中，AB=BC=AD，则∠α和∠β有什么数量关系？请结合已知条件推理出一个等式．