题目内容
2.在△ABC中,∠C=90°AB=2,AC=1.求∠A,∠B正弦,余弦,正切.分析 由勾股定理首先求得BC的长度,然后根据锐角三角函数的定义计算即可.
解答 解:如图所示:
∵在△ABC中,∠C=90°,AB=2,AC=1,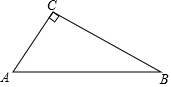
∴BC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{2}$,cosA=$\frac{AC}{AB}$=$\frac{1}{2}$,tanA=$\sqrt{3}$,sinB=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$,tanB=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查的是锐角三角函数的定义和勾股定理的应用,掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
 如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )
如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )| A. | 14 cm | B. | 17 cm | C. | 20 cm | D. | 23 cm |
11.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
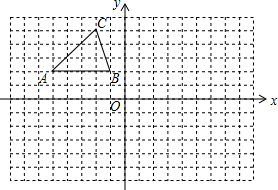 把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1(要求尺规作图,并且保留作图痕迹)
把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1(要求尺规作图,并且保留作图痕迹)