题目内容
16.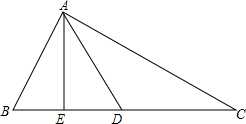 如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD,∠BAD=∠BDA,求证:AC=2AE.
如图,已知△ABC中,AD是中线,AE是△ABD的中线,BA=BD,∠BAD=∠BDA,求证:AC=2AE.
分析 由AE为中线,得到BE=ED,再由AE=EF,且夹角为对顶角相等,利用SAS得到三角形ABE与三角形FDE全等,利用全等三角形的对应边相等,对应角相等得到AB=DF,∠BAE=∠EFD,利用外角性质及等式的性质得到∠ADF=∠ADC,利用SAS得到三角形ADF与三角形ADC全等,利用全等三角形的对应边相等得到AF=AC,由AE=$\frac{1}{2}$AF,等量代换即可得证.
解答 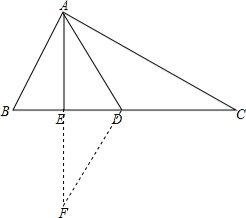 证明:延长AE到F,使EF=AE,连接DF,如图:
证明:延长AE到F,使EF=AE,连接DF,如图:
∵AE是△ABD的中线,
∴BE=ED,
在△ABE与△FDE中,
$\left\{\begin{array}{l}{BE=DE}\\{∠AEB=∠DEF}\\{AE=EF}\end{array}\right.$,
∴△ABE≌△FDE(SAS),
∴AB=DF,∠BAE=∠EFD,
∵∠ADB是△ADC的外角,
∴∠DAC=∠ACD,∠ADB=∠BAD,
∴∠BAE+∠EAD=∠BAD,∠BAE=∠EFD,
∴∠EFD+∠EAD=∠DAC+∠ACD,
∴∠ADF=∠ADC,
在△ADF与△ADC中,
$\left\{\begin{array}{l}{AD=AD}\\{∠ADF=∠ADC}\\{FD=DC}\end{array}\right.$,
∴△ADF≌△ADC(SAS),
∴AF=AC,
∵AF=AE+EF,AE=EF,
∴AC=2AE.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
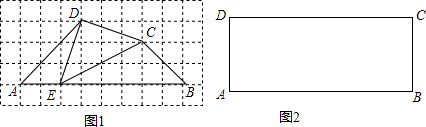
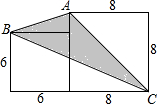 如图,求阴影部分的面积.
如图,求阴影部分的面积. 作图题
作图题