题目内容
 如图,点C为线段AB的三等分点,点D为线段AC中点.
如图,点C为线段AB的三等分点,点D为线段AC中点.(1)CD=4,求出线段AB的长度.
(2)若线段AB=a,求线段CD的长度.
考点:两点间的距离
专题:
分析:(1)根据点D为AC的中点得出AC=2DC,根据CD=4求出AC的长,再由C为AB的三等分点可知AB=3AC,由此可得出结论;
(2)根据点D为AC的中点可知DC=
AC.再由C是AB的三等分点得出AC=
AB,故可得出结论.
(2)根据点D为AC的中点可知DC=
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:(1)∵点D为AC的中点,
∴AC=2DC.
又∵CD=4,
∴AC=4×2=8.
又∵C为AB的三等分点,
∴AB=3AC=3×8=24;
(2)∵点D为AC的中点,
∴DC=
AC.
又∵C是AB的三等分点,
∴AC=
AB,
∴CD=
AC=
×
AB=
AB=
a.
∴AC=2DC.
又∵CD=4,
∴AC=4×2=8.
又∵C为AB的三等分点,
∴AB=3AC=3×8=24;
(2)∵点D为AC的中点,
∴DC=
| 1 |
| 2 |
又∵C是AB的三等分点,
∴AC=
| 1 |
| 3 |
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,将抛物线y=x2-2先向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
| A、y=(x+2)2+1 |
| B、y=(x-2)2-1 |
| C、y=(x-2)2+1 |
| D、y=(x+2)2-1 |
 如图所示的立方体,如果把它展开,可以是下列图形中的( )
如图所示的立方体,如果把它展开,可以是下列图形中的( )A、 |
B、 |
C、 |
D、 |
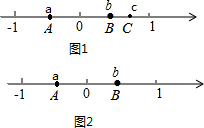 有理数a,b,c在数轴上对应的点分别为A,B,C.
有理数a,b,c在数轴上对应的点分别为A,B,C.
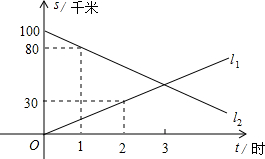 A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行使,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
A、B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行.假设他们都保持匀速行使,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数. 如图所示.
如图所示.