Question

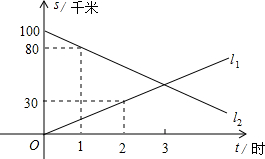A、B两地相距100千米，甲、乙两人骑车同时分别从A，B两地相向而行．假设他们都保持匀速行使，则他们各自到A地的距离s（千米）都是骑车时间t（时）的一次函数．
（1）甲的速度为

 

，乙的速度为

 

；
（2）求出：l₁和l₂的关系式；
（3）问经过多长时间两人相遇．

Answer 1

考点：一次函数的应用

专题：

分析：（1）利用图象上点的坐标得出甲、乙的速度即可；
（2）利用待定系数法求出一次函数解析式即可；
（3）利用两函数相等进而求出相遇的时间．

解答：解：（1）如图所示：甲的速度为：（100-80）÷1=20（km/h），
乙的速度为：30÷2=15（km/h），
故答案为：20km/h；15km/h；

（2）设l₁=kx，则30=k×2，解得：k=15，故l₁=15x；
设l₂=ax+b，将（0，100），（1，80），则

b=100 a+b=80

，
解得：

a=-20 b=100

，
故l₂=-20x+100；

（3）当l₁=l₂，则15x=-20x+100，
解得：x=

20

7

．
故经过

20

7

小时两人相遇．

点评：此题主要考查了一次函数的应用，根据题意求出函数解析式是解题关键．