题目内容
 填空,使证明完整,括号里面填理由.
填空,使证明完整,括号里面填理由.如下图,已知AB=DC,AC=DB.求证:∠1=∠2.
证明:在△ABC与
|
∴△ABC≌
∴∠ABC=
∴∠1=
∴∠1=∠2.
考点:全等三角形的判定与性质
专题:推理填空题
分析:找出与△ABC对应的△DCB,根据SSS方法判定三角形全等即可求得△ABC≌△DCB,根据全等三角形对应角相等的性质即可解题.
解答:解:∵△ABC和△DCB中,
,
∴△ABC≌△DCB,(SSS),
∴∠ABC=∠DCB,∠ACB=∠DBC,(全等三角形对应角相等)
∵∠1=∠ABC-∠DBC,∠2=∠DCB-∠ACB,
∴∠1=∠2.
|
∴△ABC≌△DCB,(SSS),
∴∠ABC=∠DCB,∠ACB=∠DBC,(全等三角形对应角相等)
∵∠1=∠ABC-∠DBC,∠2=∠DCB-∠ACB,
∴∠1=∠2.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABC≌△DCB是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
小军从A地沿北偏西60°方向走10m到B地,再从B地向正南方向走20m到C地,此时小军离A地( )
A、5
| ||
| B、10m | ||
| C、15m | ||
D、10
|
如图1,圆的周长为4个单位.在该圆的4等分点处分别标上字母m、n、p、q.如图2,先将圆周上表示p的点与数轴原点重合,然后将该圆沿着数轴的负方向滚动,则数轴上表示-2014的点与圆周上重合的点对应的字母是( )


| A、m | B、n | C、p | D、q |
已知二次函数y=-x2-2x+k的图象经过点A(1,y1),B(-
,y2),C(-2,y3),则下列结论正确的是( )
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y1<y3<y2 |
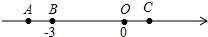 如图,数轴上点A、C对应的数分别为a、c,且a、c满足|a+4|+(c-1)2=0.,点B对应的数为-3,
如图,数轴上点A、C对应的数分别为a、c,且a、c满足|a+4|+(c-1)2=0.,点B对应的数为-3,