题目内容
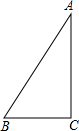
如图，△ABC中，∠BAC=90°，点G是△ABC的重心，如果AG=4，那么BC的长为考点：三角形的重心
专题：
分析：延长AG交BC于点D，根据重心的性质可知点D为BC的中点，且AG=2DG=4，则AD=6，再根据直角三角形斜边的中线等于斜边的一半即可求解．
解答：
解：如图，延长AG交BC于点D．
∵点G是△ABC的重心，AG=4，
∴点D为BC的中点，且AG=2DG=4，
∴DG=2，
∴AD=AG+DG=6，
∵△ABC中，∠BAC=90°，AD是斜边的中线，
∴BC=2AD=12．
故答案为12．
解：如图，延长AG交BC于点D．∵点G是△ABC的重心，AG=4，
∴点D为BC的中点，且AG=2DG=4，
∴DG=2，
∴AD=AG+DG=6，
∵△ABC中，∠BAC=90°，AD是斜边的中线，
∴BC=2AD=12．
故答案为12．
点评：本题考查了三角形重心的定义及性质，三角形的重心是三角形三边中线的交点，重心到顶点的距离与重心到对边中点的距离之比为2：1．同时考查了直角三角形的性质．
练习册系列答案
学业测评一课一测系列答案
相关题目
如图，方格纸中的每个小方个都是边长为一个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（-6，1），点B的坐标为（-3，1），点C的坐标为（-3，3）．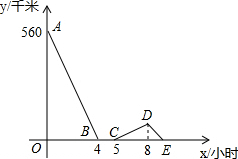
一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，下列四种说法：
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕着点C旋转90°，点A、B的对应点分别是D、E，那么tan∠ADE的值
如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、D、F和点B、C、E，如果AD=6，DF=3，BC=5，那么BE=在Rt△ABC中，∠A=90°，AC=5，BC=13，那么tanB的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若等腰三角形的一边长为3cm，另一边长为6cm，则这个三角形的周长为（ ）
| A、12cm或15cm |
| B、12cm |
| C、15cm |
| D、18cm |