题目内容
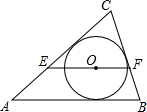 如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是
如图,O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交E、F,若AE=3,BE=2,则EF的长是考点:三角形的内切圆与内心
专题:计算题
分析:先根据内心的定义得OA平分∠BAC,则∠1=∠2,再根据平行线的性质由EF∥AB得到∠2=∠3,则∠1=∠3,根据等腰三角形的判定得AE=OE=3,用同样的方法可得OF=BF=2,然后利用EF=OE+OF求解.
解答:解:连接OA、OB,如图,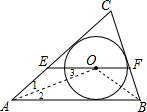
∵O是△ABC的内心,
∴OA平分∠BAC,
∴∠1=∠2,
∵EF∥AB,
∴∠2=∠3,
∴∠1=∠3,
∴AE=OE=3,
同理可得OF=BF=2,
∴EF=OE+OF=3+2=5.
故答案为5.

∵O是△ABC的内心,
∴OA平分∠BAC,
∴∠1=∠2,
∵EF∥AB,
∴∠2=∠3,
∴∠1=∠3,
∴AE=OE=3,
同理可得OF=BF=2,
∴EF=OE+OF=3+2=5.
故答案为5.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心.三角形的内心就是三角形三个内角角平分线的交点.根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
2013×2013-2013×2012-2011×2012+2012×2012的值是( )
| A、1 | B、-1 |
| C、4025 | D、4024 |
 (1)如图,在锐角△ABC中,利用三角函数的定义及勾股定理证明你的猜想;
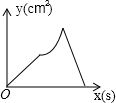
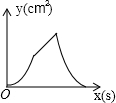
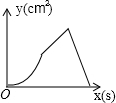
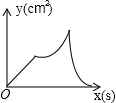
(1)如图,在锐角△ABC中,利用三角函数的定义及勾股定理证明你的猜想; 如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )
如图,在正方形ABCD中,AB=4cm,动点M从A出发,以1cm/s的速度沿折线AB-BC运动,同时动点N从A出发,以2cm/s的速度沿折线AD-DC-CB运动,M,N第一次相遇时同时停止运动.设△AMN的面积为y,运动时间为x,则下列图象中能大致反映y与x的函数关系的是( )