题目内容
如果 (α、β为锐角),则α=________,β=________.
(α、β为锐角),则α=________,β=________.
45° 60°
分析:先根据非负数的性质求出tanα及sinβ的值,再根据α、β为锐角即可求解.
解答:∵ ,
,
∴1-tanα=0,sinβ- =0,
=0,
∴tanα=1,sinβ= ,
,
∵α、β为锐角,
∴α=45°,β=60°.
故答案为:45°,60°.
点评:本题考查的是非负数的性质及特殊角的三角函数值,熟记特殊角的三角函数值是解答此题的关键.
分析:先根据非负数的性质求出tanα及sinβ的值,再根据α、β为锐角即可求解.
解答:∵
 ,
,∴1-tanα=0,sinβ-
 =0,
=0,∴tanα=1,sinβ=
 ,
,∵α、β为锐角,
∴α=45°,β=60°.
故答案为:45°,60°.
点评:本题考查的是非负数的性质及特殊角的三角函数值,熟记特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
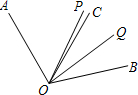 已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.
已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.

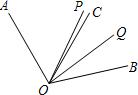 已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.
已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.