题目内容
如图，∠AOB=90°，∠AOC是∠AOB外的一个锐角，且∠AOC=30°，射线 OM平分∠BOC，ON平分∠AOC，
(1)求∠MON的度数；
(2)如果( 1)中∠AOB=α，其他条件不变，求∠MON的度数；
(3)如果( 1)中∠AOC=β（β为锐角)，其他条件不变，求∠MON的度数；
(4)从( 1 )、(2)、(3)的结果中，你能看出什么规律？
(5)线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法.请你模仿( 1 )~ (4)设计一道以线段为背景的计算题，并写出其中的规律来.
(1)求∠MON的度数；
(2)如果( 1)中∠AOB=α，其他条件不变，求∠MON的度数；
(3)如果( 1)中∠AOC=β（β为锐角)，其他条件不变，求∠MON的度数；
(4)从( 1 )、(2)、(3)的结果中，你能看出什么规律？
(5)线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法.请你模仿( 1 )~ (4)设计一道以线段为背景的计算题，并写出其中的规律来.
解：(1)因为
，
，所以
因为 OM平分
所以
因为 ON平分
，所以
.
所以
(2)当
，其他条件不变时，仿( 1)可得
(3)仿( 1 )可求得
(4)从( 1 )、(2)、(3)的结果中，可以得出一般规律：
的大小总等于
的一半， 与锐角
大小无关.
(5)问题可设计为：已知：线段AB = a，延长 AB到 C，使BC =6，点 M、N分别为 AC、BC的中点，求MN的长. 规律是：MN的长度总等于AB 的长度的一半，而与BC的长度无关.
，，所以因为 OM平分
所以因为 ON平分
，所以.所以
(2)当
，其他条件不变时，仿( 1)可得(3)仿( 1 )可求得
(4)从( 1 )、(2)、(3)的结果中，可以得出一般规律：
的大小总等于的一半， 与锐角大小无关.(5)问题可设计为：已知：线段AB = a，延长 AB到 C，使BC =6，点 M、N分别为 AC、BC的中点，求MN的长. 规律是：MN的长度总等于AB 的长度的一半，而与BC的长度无关.
练习册系列答案
相关题目
26、如图，∠AOB=90°，将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别相交于点E、F．
21、如图，∠AOB=90°，点C、D分别在OA、OB上．
（2013•泉州）如图，∠AOB=90°，∠BOC=30°，则∠AOC=
画图、证明：如图，∠AOB=90°，点C、D分别在OA、OB上．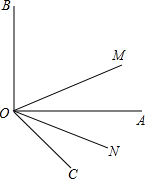
如图，∠AOB=90°，∠AOC为锐角，且ON平分∠AOC，射线OM在∠BON内部．