题目内容
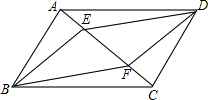已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=CF．求证：四边形BEDF是平行四边形．
考点：平行四边形的判定与性质
专题：证明题
分析：根据平行四边形的性质，可得对角线互相平分，根据对角线互相平分的四边形式平行四边形，可得证明结论．
解答：
证明：如图，连接BD设对角线交于点O．
∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD．
∵AE=CF，OA-AE=OC-CF，
∴OE=OF．
∴四边形BEDF是平行四边形．
证明：如图，连接BD设对角线交于点O．∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD．
∵AE=CF，OA-AE=OC-CF，
∴OE=OF．
∴四边形BEDF是平行四边形．
点评：本题考查了平行四边形的判定与性质，利用了平行四边形的对角线互相平分，对角线互相平分的四边形是平行四边形．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
已知直角三角形两边的长为3和4，则第三边的长为（ ）
| A、5 | ||
B、
| ||
| C、5或-1 | ||
| D、以上都不对 |
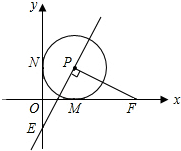已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）．
如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（
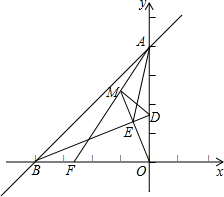在直线y=x+4与坐标轴交于A、B两点，BD平分∠ABO，交y轴于D，OE⊥BD交AB于E点，点F在OB上，且OF=AE，AF与OE相交于M点．求证：
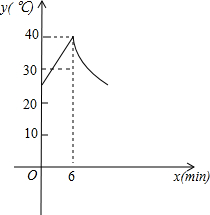墨墨在妈妈生日当天购买了一个足浴盆作为生日礼物送给妈妈．墨墨妈妈在使用该足浴盆泡脚时，最初注入的水的温度是25℃，加热6min后，水温达到最高温度40℃，然后该足浴盆自动停止加热进行保温，设定保温过程中，水温的最低温度不低于30℃，当水温降至30℃时，该足浴盆又会再次自动加热，以此循环．加热时，温度y（℃）与时间x（min）成一次函数关系；保温时，温度y（℃）与时间x（min）成反比例函数关系，第一个加热和保温过程如图所示． 
有六张完全相同的卡片，分A，B两组，每组三张，在A组的卡片上分别画上“√，×，√”，在B组的卡片上分别画上“√，×，×”，如图1所示．