题目内容
12.一个多边形,除了一个内角之外,其余内角之和为2680°,求这个内角的大小.分析 n边形的内角和是(n-2)•180°,因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和除去一个内角的值,这个值除以180度,所得数值比边数要大,大的值小于1.则用内角的和除以180所得值,加上2,比这个数大的最小的整数就是多边形的边数.
解答 解:设多边形的边数为x,由题意有
(x-2)•180=2680,
解得x=16$\frac{8}{9}$,
因而多边形的边数是17,
则这一内角为(17-2)×180°-2680°=20°.
点评 考查了多边形内角与外角,正确理解多边形的内角和是180度的整数倍,以及多边形的角的范围,是解题的关键.

练习册系列答案
相关题目
3.人体血液中每个成熟红细胞的平均直径为0.0000077米,用科学记数法表示为( )
| A. | 7.7×10-5米 | B. | 77×10-6米 | C. | 77×10-5米 | D. | 7.7×10-6米 |
7.以下列各组数为边长,不能构成直角三角形的是( )
| A. | 5,12,13 | B. | 9,12,15 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | D. | 0.3,0.4,0.5 |
2.如图,观察图形,找出规律,确定第四个图形是( )


| A. |  | B. |  | C. |  | D. |  |
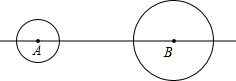 如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.
如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.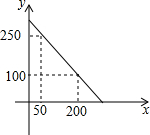 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.