题目内容
已知关于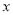
的一元二次方程
．
（
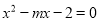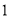）对于任意的实数
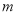，判断方程的根的情况，并说明理由．
（
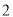）若方程的一个根为
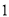，求出
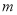的值及方程的另一个根．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案黄冈小状元口算速算练习册系列答案成功训练计划系列答案题目内容
已知关于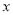的一元二次方程．
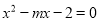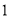（）对于任意的实数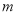，判断方程的根的情况，并说明理由．
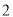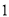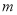（）若方程的一个根为，求出的值及方程的另一个根．
教学练新同步练习系列答案课前课后同步练习系列答案课堂小作业系列答案黄冈小状元口算速算练习册系列答案成功训练计划系列答案
．
的绳子怎样围成一个面积为
的矩形？能围成一个面积为
的矩形吗？如能，说明围法；如不能，说明理由．
内接于⊙
， 
，连接
，点
是半径
上任意一点，连接
、
，则
可能为__________度（写出一个即可）．
的根为__________．