Question

设0＜a＜b，a²+b²=4ab，则的值等于________．

Answer 1

分析：先根据完全平方公式得到（a+b）²=a²+2ab+b²，（a-b）²=a²-2ab+b²，再把a²+b²=4ab，利用0＜a＜b得到+b=，a-b=-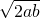，然后计算a+b除以a-b．
解答：∵（a+b）²=a²+2ab+b²，（a-b）²=a²-2ab+b²，
而a²+b²=4ab，
∴（a+b）²=a²+2ab+b²=6ab，（a-b）²=a²-2ab+b²=2ab，
∵0＜a＜b，
∴a+b=，a-b=-，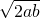
∴==-．
故答案为．
点评：本题考查了完全平方公式：（a±b）²=a²±2ab+b²．也考查了代数式的变形能力．