题目内容
如图,已知正方形ABCD的边长为4,点E、F分别从C、A两点同时出发,以相同的速度作直线运动.已知点E沿射线CB运动,点F沿边BA的延长线运动,连结DF、DE、EF,EF与对角线AC所在的直线交于点M,DE交AC于点N.
(1)求证:DE⊥DF;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式,并写出自变量的取值范围;
(3)随着点E在射线CB上运动,NA•MC的值是否会发生变化?若不变,请求出NA•MC的值;若变化,请说明理由.
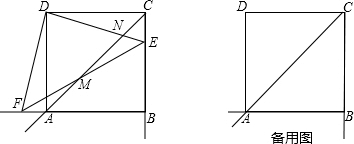
(1)求证:DE⊥DF;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式,并写出自变量的取值范围;
(3)随着点E在射线CB上运动,NA•MC的值是否会发生变化?若不变,请求出NA•MC的值;若变化,请说明理由.

考点:四边形综合题
专题:
分析:(1)易得△ADF≌△CDE,从而得到∠FDA=∠EDC,根据∠FDA+∠ADE=∠ADE+∠EDC=90°,即可证得DE⊥DF;
(2)从E作EP垂直BC,交AC于P,证得△AFM≌△PEM后得到MF=ME,从而得到△MFA中AF上的高为BE的一半,利用三角形的面积表示方法表示出两个变量之间的关系即可;
(3)证得△MCD∽△DAN后即可得到:MC:DA=DC:NA,从而将比例式转化为等积式后即可得到:MC×NA=DA×DC=4×4=16,进而说明NA和MC的乘积不发生变化.
(2)从E作EP垂直BC,交AC于P,证得△AFM≌△PEM后得到MF=ME,从而得到△MFA中AF上的高为BE的一半,利用三角形的面积表示方法表示出两个变量之间的关系即可;
(3)证得△MCD∽△DAN后即可得到:MC:DA=DC:NA,从而将比例式转化为等积式后即可得到:MC×NA=DA×DC=4×4=16,进而说明NA和MC的乘积不发生变化.
解答: 解:(1)E、F分别从C、A两点同时出发,以相同的速度作直线运动,
解:(1)E、F分别从C、A两点同时出发,以相同的速度作直线运动,
∴CE=AF,
在△ADF和△CDE中,
∴△ADF≌△CDE(SAS),
∴∠FDA=∠EDC,
∴∠FDA+∠ADE=∠ADE+∠EDC=90°,
∴DE⊥DF;
(2)当点E在BC上时,过点E作EP⊥BC,交AC于P
∵AF⊥BC,EP⊥BC,
∴AF∥EP,∠AFM=∠PEM,∠FAM=∠EPM
∵P在AC上,∠ECP=45°,
∴CE=PE,AF=PE,
在△AFM和△PEM中,
∴△AFM≌△PEM(AAS),
∴MF=ME,
∴△MFA中AF上的高为BE的一半,
∴y=
x×
(4-x)=-
x2+x(0≤x≤4);
同理,当点E在BC的延长线上时,y=
x2-x(x>4);
(3)由全等可得DE=DF,
∴△DEF为等腰直角三角形,∠DEF=45°
∵M为EF中点,
∴DM⊥EF.
∴∠MDE=45°
∵∠CMD为△AMD的外角,
∴∠CMD=∠MDA+∠DAC=∠MDA+45°,
∠ADN=∠MDA+∠MDE=∠MDA+45°,
∴∠CMD=∠ADN
∠DCM=∠DAN=45°
∴△MCD∽△DAN
∴MC:DA=DC:NA
∴MC×NA=DA×DC=4×4=16
∴NA和MC的乘积不发生变化.
 解:(1)E、F分别从C、A两点同时出发,以相同的速度作直线运动,
解:(1)E、F分别从C、A两点同时出发,以相同的速度作直线运动,∴CE=AF,
在△ADF和△CDE中,
|
∴△ADF≌△CDE(SAS),
∴∠FDA=∠EDC,
∴∠FDA+∠ADE=∠ADE+∠EDC=90°,
∴DE⊥DF;
(2)当点E在BC上时,过点E作EP⊥BC,交AC于P
∵AF⊥BC,EP⊥BC,
∴AF∥EP,∠AFM=∠PEM,∠FAM=∠EPM
∵P在AC上,∠ECP=45°,
∴CE=PE,AF=PE,
在△AFM和△PEM中,
|
∴△AFM≌△PEM(AAS),
∴MF=ME,
∴△MFA中AF上的高为BE的一半,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
同理,当点E在BC的延长线上时,y=
| 1 |
| 4 |
(3)由全等可得DE=DF,
∴△DEF为等腰直角三角形,∠DEF=45°
∵M为EF中点,
∴DM⊥EF.
∴∠MDE=45°
∵∠CMD为△AMD的外角,
∴∠CMD=∠MDA+∠DAC=∠MDA+45°,
∠ADN=∠MDA+∠MDE=∠MDA+45°,
∴∠CMD=∠ADN
∠DCM=∠DAN=45°
∴△MCD∽△DAN
∴MC:DA=DC:NA
∴MC×NA=DA×DC=4×4=16
∴NA和MC的乘积不发生变化.
点评:本题考查了四边形的综合知识,题目中涉及到了相似三角形和全等三角形的知识,难度不是很大,但涉及的知识点比较多.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠B=60°,∠BAC=80°,AD⊥BC,AE平分∠BAC,求∠DAE的度数.
如图,∠B=60°,∠BAC=80°,AD⊥BC,AE平分∠BAC,求∠DAE的度数.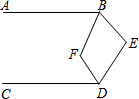 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为 如图,一棵大树在离地面9m处折断,树顶端离树底部12m,则这棵树折断之前的高度是
如图,一棵大树在离地面9m处折断,树顶端离树底部12m,则这棵树折断之前的高度是 如图,△ABC中,已知AB=8,BC=6,CA=4,D、E分别是AB、AC边的中点,则DE=
如图,△ABC中,已知AB=8,BC=6,CA=4,D、E分别是AB、AC边的中点,则DE=