题目内容
如图，⊙O是△ABC外接圆，AB=AC，P是⊙O上一点．
（1）分别出图①和图②中∠BPC的角平分线；
（2）结合图②，说明你这样理由．
（1）分别出图①和图②中∠BPC的角平分线；
（2）结合图②，说明你这样理由．
考点：圆周角定理
专题：
分析：（1）利用圆心角、弧、弦的关系，得出作法即可；
（2）利用圆周角定理得出
=
，再利用AB=AC，得出
=
，进而得出答案．
（2）利用圆周角定理得出
 |
| ABD |
|
| ACD |
|
| AB |
|
| AC |
解答：
解：（1）如图①，连接AP，即为所求角平分线；
如图②，连接AO并延长，与⊙O交于点D，连接PD，即为所求角平分线
（2）∵AD是直径，
∴半圆ABD=半圆ACD
又∵AB=AC，
∴
=
，
∴
=
，
∴∠BPD=∠CPD，
即PD平分∠BPC．
解：（1）如图①，连接AP，即为所求角平分线；如图②，连接AO并延长，与⊙O交于点D，连接PD，即为所求角平分线
（2）∵AD是直径，
∴半圆ABD=半圆ACD
又∵AB=AC，
∴
|
| AB |
|
| AC |
∴
|
| BC |
|
| BD |
∴∠BPD=∠CPD，
即PD平分∠BPC．
点评：此题主要考查了基本作图以及圆心角、弧、弦的关系等知识，熟练利用圆心角、弧、弦的关系得出是解题关键．
练习册系列答案
相关题目
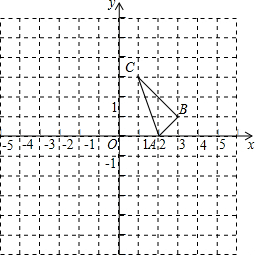如图所示的正方形网格中，△ABC的顶点均在格点上，在所给平面直角坐标系中解答下列问题：
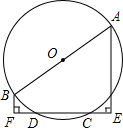已知如图，AB为⊙O直径，CD为⊙O的弦，AE⊥CD交DC延长线于E，BF⊥CD，交CD延长线于F．
如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD．已知DE=6，∠BAC+∠EAD=180°，则弦BC的弦心距等于在-3，
，0，-
四个数中，最小的数是（ ）
| 1 |
| 4 |
| 2 |
| A、-3 | ||
B、
| ||
| C、0 | ||
D、-
|
若（m-3）xn-2+3nx+3=0是关于x的一元二次方程，则（ ）
| A、m≠0，n=3 |
| B、m≠3，n=4 |
| C、m≠0，n=4 |
| D、m≠3，n≠0 |