题目内容
分解因式：20182+20182-20192．
考点：实数范围内分解因式
专题：计算题
分析：原式前两项合并，第三项变形后，利用完全平方公式变形，再利用平方差公式分解即可．
解答：解：原式=2×20182-（2018+1）2
=2×20182-20182-2×2018-1
=20182-2×2018+1-2
=（2018-1）2-2
=20172-2
=（2017+
）（2017-
）．
=2×20182-20182-2×2018-1
=20182-2×2018+1-2
=（2018-1）2-2
=20172-2
=（2017+
| 2 |
| 2 |
点评：此题考查了实数范围内分解因式，熟练掌握完全平方公式及平方差公式是解本题的关键．
练习册系列答案
相关题目
如图，⊙O中，半径OC⊥弦AB，∠BAC=20°，则∠AOC的度数是（ ）| A、30° | B、40° |
| C、50° | D、60° |
如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=3，则△ADE的周长是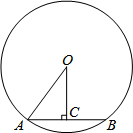
如图，AB是⊙O的弦，OC⊥AB于点C，连接OA，AB=12，⊙O半径为10．
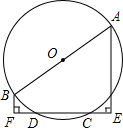已知如图，AB为⊙O直径，CD为⊙O的弦，AE⊥CD交DC延长线于E，BF⊥CD，交CD延长线于F．