题目内容
 如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且AF平分∠DAE.
如图,已知正方形ABCD中,E、F分别是BC、CD上的点,且AF平分∠DAE.(1)求证:AE=DF+BE;
(2)若AE=5,AF=6,求正方形ABCD的周长.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)延长CB到G,使BG=DF,连接AG,易证△ADF≌△ABG,得∠5=∠G,∠1=∠3,进而证明∠FAB=∠EAG,进而证明AE=EB+BG=EB+DF;
(2)由(1)可知AE=EG=5,AF=AG=6,作EH⊥AG垂足为H,利用勾股定理和等腰三角形的三线合一求得EH,进一步利用三角形AEG的面积求得AB解决问题.
(2)由(1)可知AE=EG=5,AF=AG=6,作EH⊥AG垂足为H,利用勾股定理和等腰三角形的三线合一求得EH,进一步利用三角形AEG的面积求得AB解决问题.
解答:(1)证明:延长CB到G,使BG=DF,连接AG(如图)

∵AD=AB,∠D=∠ABG=90°,
∴△ADF≌△ABG(SAS),
∴∠5=∠G,∠1=∠3,DF=BG,
∵∠1=∠2,
∴∠2=∠3,
∴∠2+∠4=∠3+∠4,
即∠FAB=∠EAG,
∵CD∥AB,
∴∠5=∠FAB=∠EAG,
∴∠EAG=∠G,
∴AE=EB+BG=EB+DF.
(2)解:如图,

作EH⊥AG垂足为H,
∵AE=EG=5,AF=AG=6,
∴EH=
=4
S△AEG=
×AG×EH=
×EG×AB
即6×4=5×AB,
∴AB=4.8,
∴正方形ABCD的周长=4.8×4=19.2.

∵AD=AB,∠D=∠ABG=90°,
∴△ADF≌△ABG(SAS),
∴∠5=∠G,∠1=∠3,DF=BG,
∵∠1=∠2,
∴∠2=∠3,
∴∠2+∠4=∠3+∠4,
即∠FAB=∠EAG,
∵CD∥AB,
∴∠5=∠FAB=∠EAG,
∴∠EAG=∠G,
∴AE=EB+BG=EB+DF.
(2)解:如图,

作EH⊥AG垂足为H,
∵AE=EG=5,AF=AG=6,
∴EH=
| 52-32 |
S△AEG=
| 1 |
| 2 |
| 1 |
| 2 |
即6×4=5×AB,
∴AB=4.8,
∴正方形ABCD的周长=4.8×4=19.2.
点评:本题考查了正方形角的性质,全等三角形的判定与性质,三角形的面积以及勾股定理等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )| A、甲运动员得分的极差大于乙运动员得分的极差 |
| B、甲运动员得分的中位数小于乙运动员得分的中位数 |
| C、甲运动员的得分平均数大于乙运动员的得分平均数 |
| D、乙运动员的成绩比甲运动员的成绩稳定 |
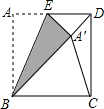 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C的度数.
如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C的度数.