题目内容
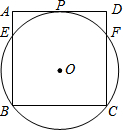 如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则
如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则考点:切线的性质,勾股定理,正方形的性质,垂径定理
专题:
分析:连接PO并延长交BC于点Q.由条件易得OP⊥AD,因而有OQ⊥BC,∴由垂径定理有PQ垂直平分BC.在Rt△OBQ中,OB2=OQ2+BQ2,若设⊙O的半径为r,有r2=(4-r)2+22,进而求出半径的大小.
解答: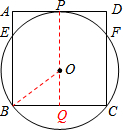 解:连接PO并延长交BC于点Q.
解:连接PO并延长交BC于点Q.
∵正方形ABCD的边AD与⊙O相切于点P
∴OP⊥AD,
∴OQ⊥BC,
∴由垂径定理有PQ垂直平分BC.在Rt△OBQ中,OB2=OQ2+BQ2,若设⊙O的半径为r,有r2=(4-r)2+22,得r=
.
故答案为:r=
.
 解:连接PO并延长交BC于点Q.
解:连接PO并延长交BC于点Q.∵正方形ABCD的边AD与⊙O相切于点P
∴OP⊥AD,
∴OQ⊥BC,
∴由垂径定理有PQ垂直平分BC.在Rt△OBQ中,OB2=OQ2+BQ2,若设⊙O的半径为r,有r2=(4-r)2+22,得r=
| 5 |
| 2 |
故答案为:r=
| 5 |
| 2 |
点评:本题考查了圆的切线性质,正方形的性质以及勾股定理的运用.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 (1)计算:(π-3)0+
(1)计算:(π-3)0+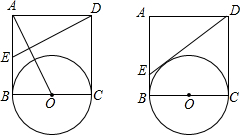
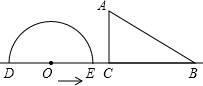 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为