题目内容
 如图,已知直角△ACB,AC=1,BC=
如图,已知直角△ACB,AC=1,BC= ,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段CA1,A1C1,C1A2,…,则第12条线段A6C6=________.
,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段CA1,A1C1,C1A2,…,则第12条线段A6C6=________.
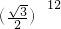
分析:根据角的正弦函数与三角形边的关系,可求出各边的长,然后再总结出规律.
解答:根据勾股定理,在直角△ACB中得,AB=2,
∴sinA=
 ,
,∴A1C=1×
 ,
,又∵A1C1⊥BC,CA1⊥AB,
∴∠A1CC1=∠A,
∴在直角△A1C1C中,根据锐角三角函数得,
A1C1=1×
 ,
,以此类推,则A6C6=1×
 =
= .
.故答案为
 .
.点评:本题主要考查了勾股定理及相似三角形的判定与性质,考查了学生运用锐角三角函数表示未知的边及分析归纳能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
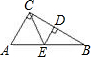 如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
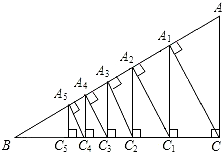 如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过CA1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段CA1,A1C1,C1A2,…,则第10条线段A5C5=
如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过CA1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段CA1,A1C1,C1A2,…,则第10条线段A5C5=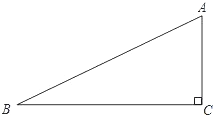 心O(要求:用尺规作图,保留作图痕迹,不写作法和证明);
心O(要求:用尺规作图,保留作图痕迹,不写作法和证明);
 如图,已知AB=AC.
如图,已知AB=AC.