题目内容
如图,已知直角三角形ABC,(Ⅰ)试作出经过点A,圆心O在斜边AB上,且与边BC相切于点E的⊙O及切点E和圆
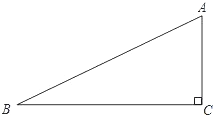 心O(要求:用尺规作图,保留作图痕迹,不写作法和证明);
心O(要求:用尺规作图,保留作图痕迹,不写作法和证明);(Ⅱ)设(Ⅰ)中所作的⊙O与边AB交于异于点A的另一点D.
求证:
(1)
| DE |
| AE |
| DE |
| BE |
(2)EC•BE=AC•BD.
分析:(Ⅰ)作∠BAC的角平分线AE交BC与E,过E点作EO垂直于BC,交AB与O,O即为所求圆心;
(Ⅱ)(1)要证
=
,由组成线段可知只需证明△BDE∽△BEA即可,而∠B为共用角,∠1为弦切角∠4所夹的弧所对的圆周角所以相等,因此有△BDE∽△BEA,即
=
;
(2)要证EC•BE=AC•BD即证
=
,由(1)知
=
,所以需证
=
,即Rt△ACE∽Rt△AED,而在这两个三角形中,都有一个直角,且易证∠1=∠3=∠2,所以可证相似,从而得出所求结论.
(Ⅱ)(1)要证
| DE |
| AE |
| BD |
| BE |
| DE |
| AE |
| BD |
| BE |
(2)要证EC•BE=AC•BD即证
| EC |
| AC |
| BD |
| BE |
| DE |
| AE |
| BD |
| BE |
| EC |
| AC |
| DE |
| AE |
解答: (Ⅰ)解:如图所示;
(Ⅰ)解:如图所示;
(Ⅱ)证明:连接DE,则∠AED=90°,
(1)∵∠4=∠2
∠B=∠B
∴△BDE∽△BEA
∴
=
;(5分)
(2)∵BC切⊙O于E,
∴OE⊥BC.
又∵AC⊥B,
∴OE∥AC.
∴∠1=∠3.
又易知∠2=∠3,
∴∠1=∠2.
又∵∠C=∠AED=90°,
∴Rt△ACE∽Rt△AED.
∴
=
.(7分)
又由(Ⅰ)知,
=
,
=
,
∴EC•BE=AC•BD.(8分)
 (Ⅰ)解:如图所示;
(Ⅰ)解:如图所示;(Ⅱ)证明:连接DE,则∠AED=90°,
(1)∵∠4=∠2
∠B=∠B
∴△BDE∽△BEA
∴
| DE |
| AE |
| BD |
| BE |
(2)∵BC切⊙O于E,
∴OE⊥BC.
又∵AC⊥B,
∴OE∥AC.
∴∠1=∠3.
又易知∠2=∠3,
∴∠1=∠2.
又∵∠C=∠AED=90°,
∴Rt△ACE∽Rt△AED.
∴
| EC |
| AC |
| DE |
| AE |
又由(Ⅰ)知,
| DE |
| AE |
| BD |
| BE |
| EC |
| AC |
| BD |
| BE |
∴EC•BE=AC•BD.(8分)
点评:此题主要考查了三角形相似和圆之间的关系,难易程度适中.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
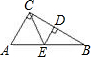 如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
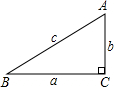 如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )
如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y=
(2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y= 如图,已知直角三角形ABC的周长为
如图,已知直角三角形ABC的周长为