题目内容
11. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=60°,则∠1=60°.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=60°,则∠1=60°.
分析 先证明∠DEF=∠EFG=∠MEF=60°,根据邻补角的定义,平行线的性质即可解决.
解答 解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠EFG=∠DEF,
∵∠DEF=∠MEF,
∴∠DEF=∠MEF=60°,
∴∠1=180°-∠DEF-∠MEF=60°,
故答案为:60°.
点评 本题考查平行线的性质、邻补角的定义、翻折变换等知识,解题的关键是利用翻折不变性找到相等的角.

练习册系列答案
相关题目
1.在平面直角坐标系中,O为原点,抛物线y=-x2+3x的对称轴l交x轴于点M,直线y=mx-2m(m<0)与该抛物线x轴上方的部分交于点A,与l交于点B,过点A作AN⊥x轴,垂足为N,则下列线段中,长度随线段ON长度的增大而增大的是( )
| A. | AN | B. | MN | C. | BM | D. | AB |
2.关于x的一元二次方程x2-x+k=0有两个实数根,则k的取值范围是( )
| A. | k$≥\frac{1}{4}$ | B. | k≥-$\frac{1}{4}$ | C. | k≤$\frac{1}{4}$ | D. | k≤-$\frac{1}{4}$ |
1.点A,B,P在同一直线上,下列说法正确的是( )
| A. | 若AB=2PA,则P是AB的中点 | B. | 若AP=PB=$\frac{1}{2}$AB,则P是AB的中点 | ||
| C. | 若AB=2PB,则P是AB的中点 | D. | 若AB=PB=$\frac{1}{2}$PA,则P是AB的中点 |
 如图是一个围棋棋盘的局部,若把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),则黑棋②的坐标是(1,-2).
如图是一个围棋棋盘的局部,若把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),则黑棋②的坐标是(1,-2).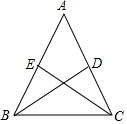 如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.


