题目内容
14.“a2=0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1.试利用“配方法”解决下列问题:(1)填空:因为x2-4x+6=(x-2)2+2;所以当x=2时,代数式x2-4x+6有最小(填“大”或“小”)值,这个最值为2.
(2)比较代数式x2-1与2x-3的大小.
分析 (1)把原式利用平方法化为完全平方算与一个常数的和的形式,利用偶次方的非负性解答;
(2)利用求差法和配方法解答即可.
解答 解:(1)x2-4x+6=(x-2)2+2,
所以当x=2时,代数式x2-4x+6有最小值,这个最值为2,
故答案为:-2;2;2;小;2;
(2)x2-1-(2x-3)
=x2-2x+2;
=(x-1)2+1>0,
则x2-1>2x-3.
点评 本题考查的是配方法的应用,掌握配方法的一般步骤是解题的关键,注意偶次方的非负性的应用.

练习册系列答案
相关题目
19.近似数1.30是由数x四舍五入得到的数,则数x的取值范围是( )
| A. | 1.25≤x<1.35 | B. | 1.295≤x<1.305 | C. | 1.25<x<1.35 | D. | 1.295<x<1.305 |
3.计算正确的是( )
| A. | $\root{3}{1}=±1$ | B. | $\sqrt{{{({-3})}^2}}=3$ | C. | $-\sqrt{0.81}=0.9$ | D. | $\sqrt{9}=±3$ |
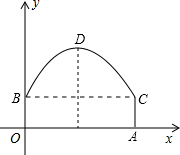 如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系
如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系