题目内容
20．
AB、CD相交于点O，DE是△DOB的角平分线，若∠B=∠C，∠A=50°，则∠EDB=25°．
分析 根据三角形的内角和得到∠A=∠BOD=50°，然后由角平分线的定义即可得到结论．
解答 解：∵∠B=∠C，∠AOC=∠BOD，
∴180°-∠C-∠AOC=180°-∠B-∠BOD，
即∠A=∠BDO=50°，
∵DE是△DOB的角平分线，
∴∠EDB=$\frac{1}{2}∠$BDO=25°．
故答案为：25°．
点评 本题考查了三角形的内角和，角平分线的定义，熟练掌握三角形的内角和是解题的关键．
练习册系列答案
相关题目
8．某自行车厂一周计划生产700辆自行车，平均每天生产100辆，由于各种原因实际每天生产量与计划量相比有出入．表是某周的生产情况（超产为正、减产为负）：
（1）这一周最后三天共生产297辆自行车；
（2）这一周产量最多的一天比产量最少的一天多生产18辆自行车；
（3）若该厂实行“每周计件工资制”，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -2 | -4 | +7 | -8 | +10 | -5 |
（2）这一周产量最多的一天比产量最少的一天多生产18辆自行车；
（3）若该厂实行“每周计件工资制”，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
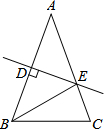如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为30°．