题目内容
11.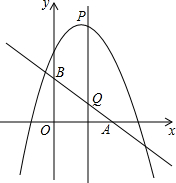 如图,已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B,P是抛物线y=-$\frac{1}{2}$x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q,则当PQ=BQ时,a的值是-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.
如图,已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B,P是抛物线y=-$\frac{1}{2}$x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q,则当PQ=BQ时,a的值是-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.
分析 设点P的坐标为(a,-$\frac{1}{2}$a2+2a+5),分别表示出B、Q的坐标,然后根据PQ=BQ,列方程求出a的值.
解答 解:设点P的坐标为(a,-$\frac{1}{2}$a2+2a+5),
则点Q为(a,-$\frac{3}{4}$a+3),点B为(0,3),
①当点P在点Q上方时,BQ=$\sqrt{{a}^{2}+(\frac{3}{4}a)^{2}}$=|$\frac{5}{4}$a|,
PQ=-$\frac{1}{2}$a2+2a+5-(-$\frac{3}{4}$a+3)=-$\frac{1}{2}$a2+$\frac{11}{4}$a+2,
∵PQ=BQ,
当a>0时,
∴$\frac{5}{4}$a=-$\frac{1}{2}$a2+$\frac{11}{4}$a+2,
整理得:a2-3a-4=0,
解得:a=-1(舍去)或a=4,
当a<0时,则-$\frac{5}{4}$a=-$\frac{1}{2}$a2+$\frac{11}{4}$a+2,
解得:a=4+2$\sqrt{5}$(舍去)或a=4-2$\sqrt{5}$;
②当点P在点Q下方时,BQ=$\sqrt{{a}^{2}+(\frac{3}{4}a)^{2}}$=|$\frac{5}{4}$a|,
PQ=-$\frac{3}{4}$a+3-(-$\frac{1}{2}$a2+2a+5)=$\frac{1}{2}$a2-$\frac{11}{4}$a-2,
由题意得,PQ=BQ,
当a>0时,
则$\frac{5}{4}$a=$\frac{1}{2}$a2-$\frac{11}{4}$a-2,
整理得:a2-8a-4=0,
解得:a=4+2$\sqrt{5}$或a=4-2$\sqrt{5}$(舍去).
当a<0时,则-$\frac{5}{4}$a=$\frac{1}{2}$a2-$\frac{11}{4}$a-2,
解得:a=-1或a=4(舍去),
综上所述,a的值为:-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.
故答案为:-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.
点评 本题考查了二次函数的综合知识,涉及了二次函数与一次函数的交点问题,以及两点间的距离,解答本题的关键是设出点P的坐标,表示出PQ、BQ的长度,然后根据PQ=BQ,分情况讨论并求解,难度一般.

 字词句段篇系列答案
字词句段篇系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
 如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )| A. | 6$\sqrt{3}$米 | B. | 6米 | C. | 3$\sqrt{3}$米 | D. | 3米 |
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2•a4=a6 | C. | (2a2)3=2a6 | D. | (a+2)2=a2+4 |
 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )| A. | 88° | B. | 92° | C. | 106° | D. | 136° |

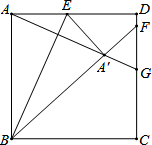 如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.
如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.