题目内容
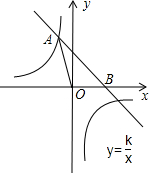
10. 如图所示,已知A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
如图所示,已知A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )| A. |  | B. |  | C. |  | D. |  |
分析 结合点P的运动,将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式,通过图形的特点分析出面积变化的趋势,从而得到答案.
解答 解:设∠AOM=α,点P运动的速度为a,
当点P从点O运动到点A的过程中,S=$\frac{(at•cosα)•(at•sinα)}{2}$=$\frac{1}{2}$a2•cosα•sinα•t2,
由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;
当点P从A运动到B时,由反比例函数性质可知△OPM的面积为$\frac{1}{2}$k,保持不变,
故本段图象应为与横轴平行的线段;
当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,
故本段图象应该为一段下降的线段;
故选:D.
点评 本题考查了反比例函数图象性质、锐角三角函数性质,解题的关键是明确点P在O→A、A→B、B→C三段位置时三角形OMP的面积计算方式.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
1.在2017年全国两会政府工作报告中,李克强总理指出国内生产总值达到744000亿元,增长6.7%,名列世界前茅,对全球经济增长的贡献率超过30%,数字744000用科学记数法可表示为( )
| A. | 7.44×105 | B. | 0.744×106 | C. | 744×103 | D. | 7.11×106 |
19.在一个不透明的盒子里装有3个分别标有数字1,2,3的小球,它们除数字外其他均相同,充分摇匀后,先摸出1个球不放回,再摸出1个球,那么这两个球上的数字之和为奇数的概率为$\frac{2}{3}$.
20.有5张看上去无差别的卡片,上面分别写着0,π,$\sqrt{2}$,$\frac{1}{8}$,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,已知直线y=-x+4与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,a),并且与x轴相交于点B.
如图,已知直线y=-x+4与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,a),并且与x轴相交于点B.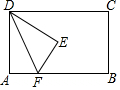 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则tan∠ADF=$\frac{\sqrt{3}}{3}$.
如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则tan∠ADF=$\frac{\sqrt{3}}{3}$.