题目内容
 如图,AD∥BF,AB⊥AD,点B、E关于AC对称,点E、F关于BD对称,则tan∠ADB=
如图,AD∥BF,AB⊥AD,点B、E关于AC对称,点E、F关于BD对称,则tan∠ADB=考点:轴对称的性质,解直角三角形
专题:
分析:根据轴对称的性质可得∠ABE=∠AEB=45°,∠FBD=∠EBD,再根据两直线平行,内错角相等可得∠FBD=∠EDB,再求出∠EBD=∠EDB,然后根据等角对等边可得BE=DE,设AB=x,表示出AE、BE,再求出AD,然后根据锐角的正切等于对边比邻边列式计算即可得解.
解答:
解:∵AB⊥AD,点B、E关于AC对称,
∴∠ABE=∠AEB=45°,
∵点E、F关于BD对称,
∴∠FBD=∠EBD,
∵AD∥BF,
∴∠FBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
设AB=x,则AE=x,
BE=
AB=
x,
所以,AD=AE+DE=x+
x,
所以,tan∠ADB=
=
=
-1.
故答案为:
-1.
∴∠ABE=∠AEB=45°,
∵点E、F关于BD对称,
∴∠FBD=∠EBD,
∵AD∥BF,
∴∠FBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
设AB=x,则AE=x,
BE=
| 2 |
| 2 |
所以,AD=AE+DE=x+
| 2 |
所以,tan∠ADB=
| AB |
| AD |
| x | ||
x+
|
| 2 |
故答案为:
| 2 |
点评:本题考查了轴对称的性质,平行线的性质,锐角三角函数的定义,熟记性质是解题的关键,难点在于求出BE=DE.

练习册系列答案
相关题目
下列多项式中,能用完全平方公式分解因式的是( )
| A、a2+4 | ||
| B、a2+ab+b2 | ||
| C、a2+4a+b2 | ||
D、x2-x+
|
已知点A的坐标为(1,4),则点A关于y轴对称的点的横坐标为( )
| A、1 | B、-1 | C、4 | D、-4 |
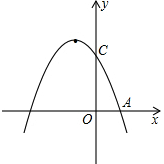 已知:如图,抛物线y=-x2-2x+m与x轴交于A(1,0)点,与y轴交于点C,另有一条直线l的解析式为y=2x+n.
已知:如图,抛物线y=-x2-2x+m与x轴交于A(1,0)点,与y轴交于点C,另有一条直线l的解析式为y=2x+n. 小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有
小明设计了某个产品的包装盒,由于粗心,少设计了其中一部分,请你把它补上,使其成为一个两面均有盖的正方体盒子,共有