题目内容
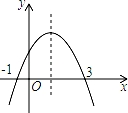
已知抛物线y=ax2+bx+c的部分图象如图所示，则不等式ax2+bx+c＞0的解集为 ．
﹣1＜x＜3 ．
【考点】二次函数与不等式（组）．
【分析】由图可知，该函数的对称轴是x=1，则x轴上与﹣1对应的点是3．观察图象可知y＞0时x的取值范围
【解答】解：已知抛物线与x轴的一个交点是（﹣1，0）对称轴为x=1，
根据对称性，抛物线与x轴的另一交点为（3，0），
观察图象，当y＞0时，﹣1＜x＜3，
∴不等式ax2+bx+c＞0的解集为：﹣1＜x＜3，
故答案为：﹣1＜x＜3．
【点评】本题考查了二次函数与不等式，解答此题的关键是根据二次函数的对称轴与对称性，找出抛物线y=ax2+bx+c的完整图象．
的图象经过点P(－1，1)，则k的值是某校开展了主题为“梅山文化知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了不完整的表格和扇形统计图(如图6).
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
图6
根据以上提供的信息解答下列问题：
(1)本次问卷调查共抽取的学生数为___ _人，表中m的值为__ __；
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数，并补全扇形统计图；
(3)若该校有学生2000人，请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少？
－4n)