题目内容
小明在刚结束的校冬季田径运动会上投掷铅球，在草地上砸出一个最大深度为2cm，半径为4cm的圆坑，则铅球直径为 ．
考点：垂径定理的应用,勾股定理
专题：
分析：根据题意画出草图，建立数学模型，根据勾股定理和垂径定理求解．
解答：
解：设该铅球的半径是r．
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中，
AD=BD=2cm，DO=（r-2）cm，
根据勾股定理，得r2=（r-2）2+42，
解得：r=5，
故2r=10．
故答案为：10cm．
解：设该铅球的半径是r．在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中，
AD=BD=2cm，DO=（r-2）cm，
根据勾股定理，得r2=（r-2）2+42，
解得：r=5，
故2r=10．
故答案为：10cm．
点评：此题主要考查了垂径定理的应用以及勾股定理，能够从实际问题中抽象出几何图形，再进一步根据勾股定理以及垂径定理进行计算．
练习册系列答案
阅读快车系列答案
相关题目
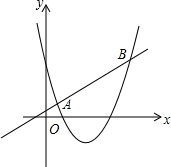已知关于x的二次函数y=x2-2mx+m2+m的图象与关于x的函数y=x+1的图象交于两点A（x1，y1）、B（x2，y2）；（x1＜x2），m为任何值时，猜想AB的长是否不变？并证明你的猜想．
如图，梯形ABCD中，AB∥CD，∠B=90°，E为BC上一点，且∠AED=90°，若AB=5，BC=12，CD=7，求BE的长．
如图，∠1与∠3是同位角吗？∠2与∠4是同位角吗？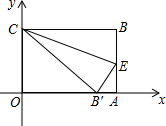
如图，在直角坐标系中放入一个边长OC为9的矩形纸片ABCO．将纸片翻折后，点B恰好落在x轴上，记为B′，折痕为CE，已知tan∠OB′C=