题目内容
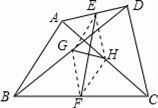
.如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件 时,有EF⊥GH.


AB=CD
【考点】中点四边形.
【分析】连接EG、GF、FH、HE,根据三角形中位线定理得到EG∥AB,EG=
 AB,GF∥CD,GF=
AB,GF∥CD,GF=
 CD,FH∥AB,FH=
CD,FH∥AB,FH=
 AB,EH∥CD,EH=
AB,EH∥CD,EH=
 CD,得到平行四边形EGFH,根据菱形的判定和性质证明结论.
CD,得到平行四边形EGFH,根据菱形的判定和性质证明结论.
【解答】解:当AB=CD时,EF⊥GH.
利用:连接EG、GF、FH、HE,
∵E、G分别是AD、BD的中点,
∴EG∥AB,EG=
 AB,
AB,
同理GF∥CD,GF=
 CD,FH∥AB,FH=
CD,FH∥AB,FH=
 AB,EH∥CD,EH=
AB,EH∥CD,EH=
 CD,
CD,
∴EG∥FH,EG=FH,
∴四边形EGFH是平行四边形,
当AB=CD时,EG=EH,
∴四边形EGFH是菱形,
∴EF⊥GH.
故答案为:AB=CD.


练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.
| 每周课外阅读时间(小时) | 0~1 | 1~2 (不含1) | 2~3 (不含2) | 超过3 |
| 人 数 | 7 | 10 | 14 | 19 |
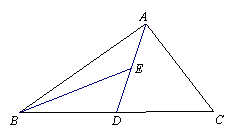 (3) 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F,求△BCF的面积。(友情提示:两条平行线间的距离处处相等.)
(3) 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F,求△BCF的面积。(友情提示:两条平行线间的距离处处相等.)


 ÷3
÷3
 ×
×



 (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )

