题目内容
1.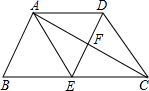 四边形ABCD中,AD∥BC,DE⊥AC,∠BAC=90°,E是BC的中点,四边形AECD是菱形.
四边形ABCD中,AD∥BC,DE⊥AC,∠BAC=90°,E是BC的中点,四边形AECD是菱形.
分析 由条件可先证得DE∥AB,可证得四边形ABED为平行四边形,可求得AD=BE,利用直角三角形的性质可求得BE=EC=AE,则可证得四边形AECD为菱形.
解答 证明:
∵DE⊥AC,
∴∠EFC=∠BAC=90°,
∴DE∥AB,且AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵E为BC中点,且∠BAC=90°,
∴AE=EC=BE,
∴AD=EC,且AD∥EC,
∴四边形AECD为平行四边形,且AE=EC,
∴四边形AECD为菱形.
点评 本题主要考查菱形的判定,掌握菱形的判定方法是解题的关键,即先证明四边形是平行四边形,再证明有一组邻边相等或对角线互相垂直即可.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
1.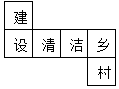 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )
 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )| A. | 清 | B. | 洁 | C. | 乡 | D. | 村 |
6.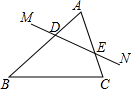 如图,已知直线MN分别交△ABC的两条边AB、AC于点D和点E,那么与∠ADE成内错角关系的角是( )
如图,已知直线MN分别交△ABC的两条边AB、AC于点D和点E,那么与∠ADE成内错角关系的角是( )
 如图,已知直线MN分别交△ABC的两条边AB、AC于点D和点E,那么与∠ADE成内错角关系的角是( )
如图,已知直线MN分别交△ABC的两条边AB、AC于点D和点E,那么与∠ADE成内错角关系的角是( )| A. | ∠BDM | B. | ∠CED | C. | ∠AED | D. | ∠AEN |
13.计算$\sqrt{27}$-$\sqrt{3}$的结果是( )
| A. | 24 | B. | $\sqrt{24}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
 如图,AB∥CD,AE、DF分别是∠BAD、∠CDA的角平分线,那么AE与DF是否平行?请说明理由.
如图,AB∥CD,AE、DF分别是∠BAD、∠CDA的角平分线,那么AE与DF是否平行?请说明理由.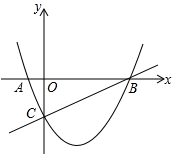 如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.
如图,已知抛物线y=ax2-x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点.求抛物线的解析式.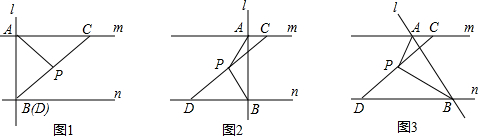
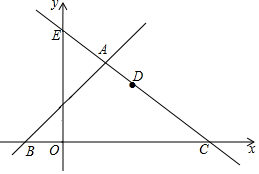 如图,在平面直角坐标系中,直线EC与两坐标轴分别交于E(0,3)、C(4,0)两点,与直线y=x+1交于点A,直线y=x+1交x轴于点B,点D是直线AC上的一个动点.
如图,在平面直角坐标系中,直线EC与两坐标轴分别交于E(0,3)、C(4,0)两点,与直线y=x+1交于点A,直线y=x+1交x轴于点B,点D是直线AC上的一个动点.