题目内容

2．计算：
（1）（$\sqrt{2}$-$\sqrt{\frac{1}{2}}$）-（$\frac{\sqrt{24}+\sqrt{6}}{\sqrt{3}}$）
（2）（1-$\sqrt{5}$）（-1-$\sqrt{5}$）+（-2）-1-$\root{3}{27}$．

分析 （1）原式去括号合并即可得到结果；
（2）原式利用平方差公式，负整数指数幂法则，以及立方根定义计算即可得到结果．

解答 解：（1）原式=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$-$\sqrt{2}$=-$\frac{5\sqrt{2}}{2}$；
（2）原式=5-1-$\frac{1}{2}$-3=$\frac{1}{2}$．

点评 此题考查了实数的运算，以及负整数指数幂，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目

化简的结果是( )

A. 4a B. 16 C. 2a D. 2a
14．（1）解方程组：
①$\left\{{\begin{array}{l}{y=2x-3}\\{4x-3y=1}\end{array}}\right.$
②$\left\{{\begin{array}{l}{x+3y=0}\\{\frac{x}{3}-\frac{y-1}{2}=1}\end{array}}\right.$
（2）解不等式组$\left\{\begin{array}{l}5x-2＞3（x-2）\\ 1-x≥x-5\end{array}$并把解集在数轴上表示出来．
11．下列各式中正确的是（　　）
A．2-3=8B．-2-3=$\frac{1}{8}$C．-2-3=-$\frac{1}{8}$D．（2017-π）0=0
17．下列函数中，y关于x的二次函数的是（　　）
A．y=x3+2x2+3B．y=-$\frac{1}{{x}^{2}}$C．y=x2+xD．y=mx2+x+1
6．已知，△ABC中，∠BAC=90°，AB=AC，点D为AC边上的一个动点，点E在BC边的延长线上，∠CAE=∠CBD．
（1）如图1，若点D为AC边的中点，求证：BC=2CE；
（2）如图2，若$\frac{AD}{AC}$=$\frac{1}{3}$，试猜想线段BC与CE的数量关系，并说明理由；
（3）若$\frac{AD}{AC}$=$\frac{1}{n}$，则$\frac{BC}{CE}$的值为$\frac{2}{n-1}$．
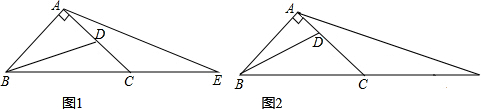
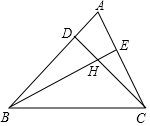13．如图锐角△ABC，若∠ABC=40°，∠ACB=70°，点D、E在边AB、AC上，CD与BE交于点H．
（l）若BE⊥AC，CD⊥AB，求∠BHC的度数．
（2）若BE、CD平分∠ABC和∠ACB，求∠BHC的度数．
9．如图，A、B分别是x轴上位于原点左右两侧的两点，点P（a，4）在第一象限内，一过原点的直线y=2x与直线BD、直线AC同时过点P，直线BD交y轴于点D，且线段AO=2．
（1）求△AOP的面积；
（2）若S△BOP=3S△AOP，求直线BD的解析式．
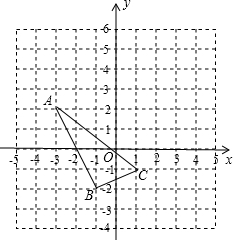10．如图，将△ABC向右平移3个单位长度，再向上平移2个单位长度，得到△A1B1C1，完成下列问题：
（1）画出平移后的△A1B1C1；
（2）写出点C1的坐标；
（3）求出△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网