题目内容
一个圆锥的侧面积是底面积的5倍,则这个圆锥的侧面展开图的圆心角等于 度.
考点:圆锥的计算
专题:
分析:根据圆锥侧面积是底面积的2倍得到圆锥底面半径和母线长的关系,进而根据圆锥的弧长等于底面周长得到圆锥的侧面展开图的圆心角.
解答:解:设母线长为R,底面半径为r,则底面周长=2πr,底面面积=πr2,侧面面积=πrR.
∵侧面积是底面积的5倍,
∴R=5r.
设圆心角为n.
∴
=2πr=
πR,
∴n=72°,
故答案为:72.
∵侧面积是底面积的5倍,
∴R=5r.
设圆心角为n.
∴
| nπR |
| 180 |
| 2 |
| 5 |
∴n=72°,
故答案为:72.
点评:本题利用了扇形面积公式,弧长公式,圆的周长公式求解.

练习册系列答案
相关题目
已知式子2x2-5x+3的值为9,则x2-
x+6的值为( )
| 5 |
| 2 |
| A、13 | B、12 | C、9 | D、7 |
在式子a+b,3xy,
,n,-8,
,
中,单项式的个数是( )
| y |
| x |
| m-n |
| 3 |
| x |
| 2 |
| A、4 | B、5 | C、6 | D、7 |
 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= 如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是
如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是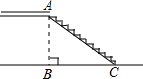 如图,市政府准备修建一座的过街天桥,已知地面BC为8米,则桥的坡面AC是10米.则此街道的交通“限高”为
如图,市政府准备修建一座的过街天桥,已知地面BC为8米,则桥的坡面AC是10米.则此街道的交通“限高”为 如图,已知在△ABC中,AB=AC,sinB=
如图,已知在△ABC中,AB=AC,sinB= 有理数a、b、c在数轴上的位置如图所示,其中|a|=|c|,化简式子
有理数a、b、c在数轴上的位置如图所示,其中|a|=|c|,化简式子