Question

【题目】综合与实践

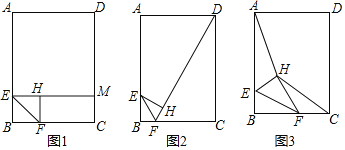
如图①，在中中，，，，过点作于，将绕点逆时针方向旋转，得到，连接，，记旋转角为．

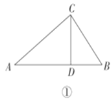
（1）问题发现

如图②，当时，__________；如图③，当时，__________．

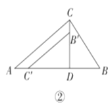
（2）拓展探究

试判断：当时，的大小有无变化？请仅就图④的情形给出证明．

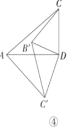
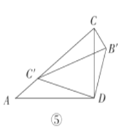
（3）问题解决

如图⑤，当绕点逆时针旋转至点落在边上时，求线段的长．

Answer 1

【答案】（1），；（2）无变化，理由详见解析；（3）．

【解析】

（1）首先利用勾股定理可求出AB的值，再根据三角形面积求出CD的值，再次利用勾股定理求出AD、BD的值，再分情况进一步得出的值即可；

（2）根据旋转的性质可得出，，再证明即可得出结论；

（3）过点作于，证，推出，得出，继而得到，再根据，即可得出答案．

解：（1）∵，，

∴

∵

∴

∴

当时，

∴

当时，

∴

故答案为：；；

（2）无变化．

证明：∵在中，，，，

∴．

∵，

∴．

∵，，

∴．

∴，即．

∴，．

∴．

由旋转可知，，．

∴．

∵，

∴．

∴．

∴．

（3）如图，过点作于．

∵，

∴．

∵，，

∴．

∴，即．

∴．

∴．

∴．

∵，

∴．