题目内容
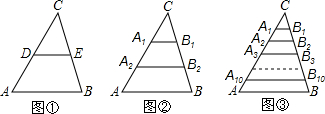
1.已知:△ABC中,AB=10(1)如图①,若点D、E分别是AC、BC边的中点,求DE的长;
(2)如图②,若点A1、A2把AC边三等分,点B1、B2把BC边三等分,求A1B1+A2B2的值;
(3)如图③,若点A1、A2、…、A10把AC边十一等分,点B1、B2、…、B10把BC边十一等分,根据你所发现的规律,直接写出A1B1+A2B2+…+A10B10=50.
分析 (1)根据三角形的中位线定理进行计算;
(2)设A1B1=x,根据三角形的中位线定理和梯形的中位线定理列方程求解;
(3)根据(1)和(2)的解答过程,发现每一条线段的长和总线段之间的关系:有n等分点的时候,则A1B1=$\frac{10}{n}$,A2B2=$\frac{20}{n}$,…An-1Bn-1=$\frac{10(n-1)}{n}$.
解答 解:(1)∵D、E分别是AC、BD的中点,且AB=10,
∴DE=$\frac{1}{2}$AB=5;
(2)设A1B1=x,则A2B2=2x.
∵A1、A2是AC的三等分点,且A1B1∥A2B2∥AB,
∴A2B2是梯形A1ABB1的中位线,即:x+10=4x,得x=$\frac{10}{3}$,
∴A1B1+A2B2=10;
(3)同理可得:A1B1+A2B2+…+A10B10=$\frac{10}{11}$+$\frac{20}{11}$+$\frac{30}{11}$+…+$\frac{100}{11}$=50.
故答案为:50.
点评 本题考查了三角形的中位线定理和梯形的中位线定理,找出规律是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
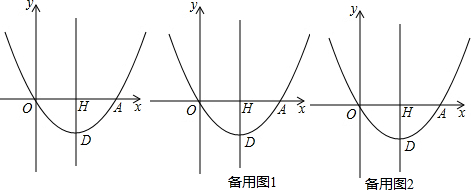
9.已知抛物线的顶点坐标为(1,9),它与x轴交于A、B两点,A点的坐标为(-2,0),则B点坐标为( )
| A. | (1,0) | B. | (2,0) | C. | (3,0) | D. | (4,0) |
 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为15π.
一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为15π.